7. Surface Integrals

7.1. Vector Flux

We can look at surface integrals next, these are the natural extension to line integrals, now we require a two variable parameterisation, here we will use \((u,\, v)\) as variables which can parameterise the surface \(S\) we are interested in.

Lets start by thinking about some surface, as depicted in Fig. 7.1, which we will break up into infinitesimal area elements \(\mathrm{d}S\). Just like we can write infinitesimal area elements \(\mathrm{d}A = \mathrm{d}x\,\mathrm{d}y\) in Cartesian coordinates (and in polar coordinates \(\mathrm{d}A = r\,\mathrm{d}r\,\mathrm{d}\theta\)), we can break up this surface using the parameterisation \((u,\,v)\).

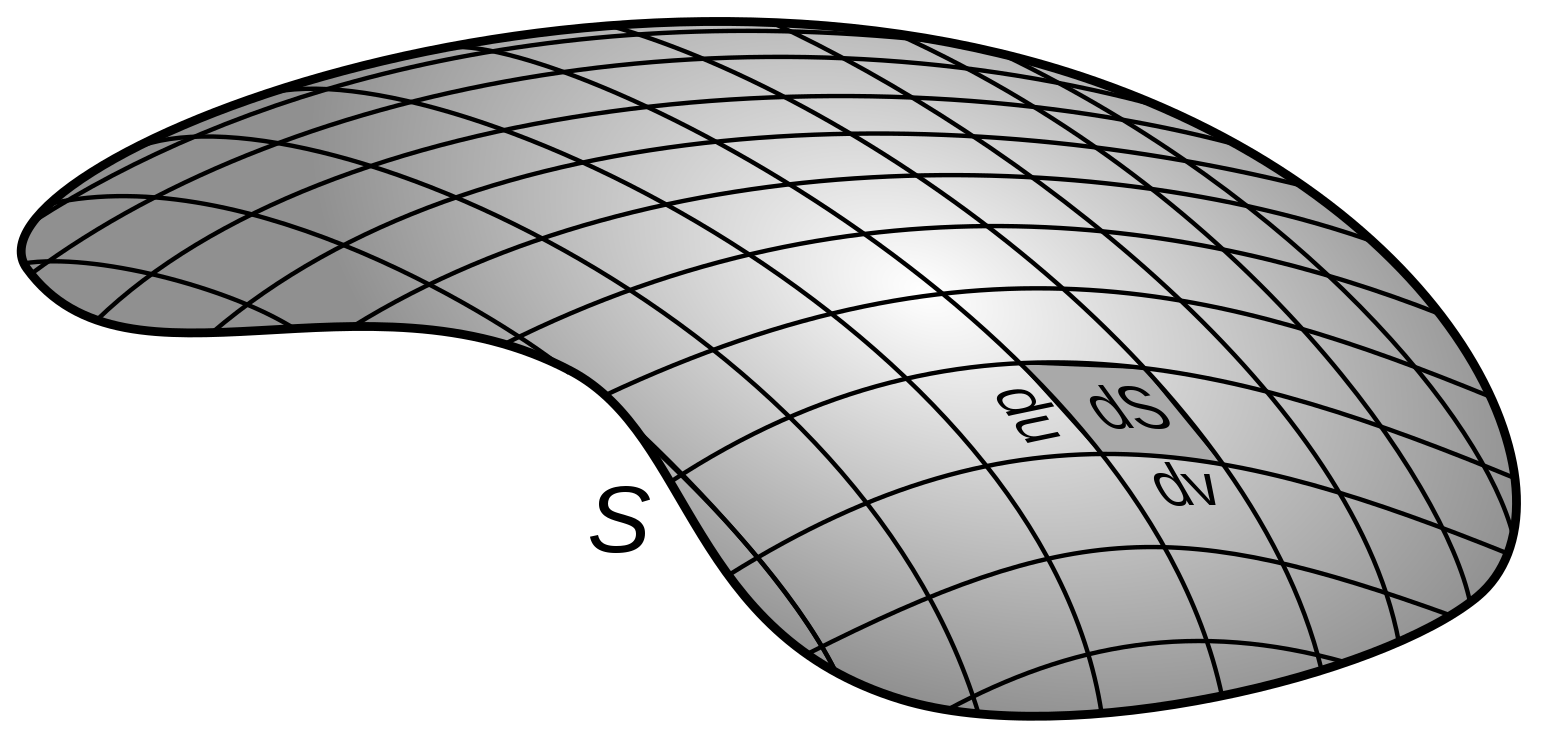
Fig. 7.1 Some general surface \(S\) broken up into infinitesimal area elements \(\mathrm{d}S\).

We can think about the effect of some vector field crossing this surface, as depicted in Fig. 7.2.

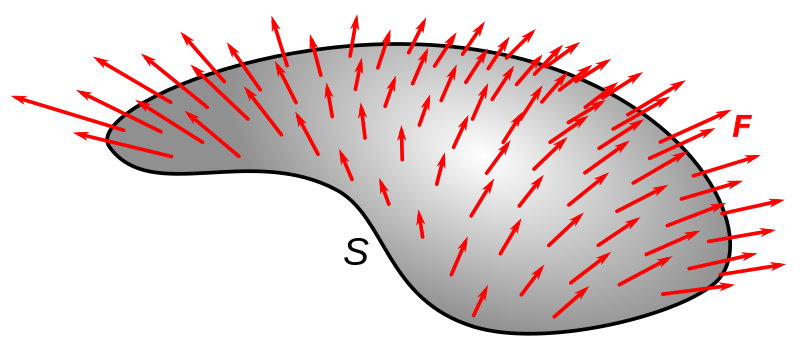
Fig. 7.2 A vector field \({\bf F}\) crossing a surface \(S\).

To find the total contribution of the vector field actually going through a surface area element, we need to think about the components of the vector field.

We can decompose \({\bf F} = {\bf F}_\bot + {\bf F}_{\parallel}\) components, as depicted in Fig. 7.3

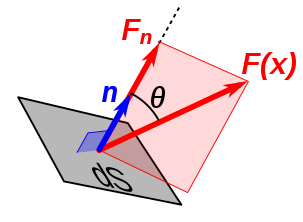
Fig. 7.3 Decomposition of vector field \({\bf F}\) into perpendicular components with respect to a surface area element \(\mathrm{d}S\).

In order to find the components that cross through the surface, \({\bf F}_{\bot}\), we need a surface normal vector. We know that in order to find a surface normal, we can do the cross product of two vectors that live on the surface.

We also that the effect of differentiating vector \({\bf r}\) with respect to some parameter produces a vector which points in the direction where \({\bf r}\) is maximised with respect to that parameter and crucially lives on the surface \(S({\bf r})\), so we use the derivatives with respect to the two parameters \((u,\,v)\):

\[{\bf n} = \left( \frac{\partial {\bf r}}{\partial u}\right)\times \left(\frac{\partial {\bf r}}{\partial v} \right)\]

This means that combination of the vector field with the area element \(|\mathrm{d}{\bf S}| = \mathrm{d}u\,\mathrm{d}v\) will be:

\[\iint_S {\bf F} \cdot \mathrm{d}{\bf S} = \iint_S {\bf F}\cdot \left( \frac{\partial {\bf r}}{\partial u}\times \frac{\partial {\bf r}}{\partial v} \right)\,\mathrm{d}u\,\mathrm{d}v\]

We call this the flux of the vector field \({\bf F}\) crossing the surface \(S\).

Definition

We can define:

\[\iint_S {\bf F} \cdot \mathrm{d}{\bf S} = \iint_S {\bf F} \cdot \left( \frac{\partial {\bf r}}{\partial u}\times \frac{\partial {\bf r}}{\partial v} \right)\,\mathrm{d}u\,\mathrm{d}v\]

as a vector surface integral along some surface \(S\), which is parameterised by variables \((u,\, v)\).

We can also define a scalar surface integral:

\[\iint_S f\left|\frac{\partial {\bf r}}{\partial u}\times \frac{\partial {\bf r}}{\partial v} \right|\,\mathrm{d}u\,\mathrm{d}v\]

along some surface \(S\), which is parameterised by variables \((u,\, v)\).

7.1.1. Calculating Surface Integrals

Similar to line integrals, we must parameterise the surface \(S\) in order for this integral to be possible, so we will pick \(S = S({\bf r})\) such that \({\bf r} = {\bf r}(u,\, v)\) with \(a \leq u \leq b,\, c \leq v \leq d\). Hence to actually calculate these we will have:

\[\begin{split}I_f &= \int_{a}^{b} \,\mathrm{d}u\,\int_{c}^{d} \, \mathrm{d}v\,f({\bf r}(u,\,v)\,\left| \frac{\partial {\bf r}}{\partial u} \times \frac{\partial {\bf r}}{\partial v} \right|\\ I_{\bf G} &= \int_{a}^{b} \,\mathrm{d}u\,\int_{c}^{d} \, \mathrm{d}v\,{\bf F}({\bf r}(u,\,v))\cdot\left(\frac{\partial {\bf r}}{\partial u} \times \frac{\partial {\bf r}}{\partial v} \right)\end{split}\]

7.2. Surfaces of the form \(z = f(x,\, y)\)

A different sort of example is where we have a 2D scalar field \(f(x,\,y)\) and we plot this as a surface \(z = f(x,\,y)\).
Here the parameterisation of the surface is given for free in terms of \(x,\,y\).

The surface has a coordinate vector of the form:

\[\begin{split}{\bf r}(x,\,y) = \begin{pmatrix} x \\ y \\ f(x,\, y) \end{pmatrix}\end{split}\]

and the infinitesimal area element is given by:

\[\begin{split}\mathrm{d}{\bf S} &= \left(\frac{\partial {\bf r}}{\partial x} \times \frac{\partial {\bf r}}{\partial y}\right)\,\mathrm{d}x\,\mathrm{d}y = \begin{pmatrix} 1 \\ 0 \\ \partial z/\partial x \end{pmatrix} \times \begin{pmatrix} 0 \\ 1 \\ \partial z/\partial y \end{pmatrix}\,\mathrm{d}x\,\mathrm{d}y \\ &= \begin{vmatrix} \hat{\bf x} & \hat{\bf y} & \hat{\bf z} \\ 1 & 0 & f_x \\ 0& 1& f_y\end{vmatrix}\,\mathrm{d}x\,\mathrm{d}y = \begin{pmatrix} -f_x \\ -f_y \\ 1 \end{pmatrix}\,\mathrm{d}x\,\mathrm{d}y\end{split}\]

If we have a scalar surface integral, then area element will involve the magnitude of this vector:

\[\mathrm{d}{S} = \left(\sqrt{{f_x}^2 + {f_y}^2 + 1}\right)\,\mathrm{d}x\,\mathrm{d}y\]

Worked example

1. Lets find the surface area of a sphere with radius \(R\). The most natural choice of parameters here would be the angles \((\theta,\, \phi)\):

\[\begin{split}{\bf r}(\theta,\,\phi) = \begin{pmatrix} R\sin(\theta)\cos(\phi) \\ R \sin(\theta)\sin(\phi)\\ R \cos(\theta)\end{pmatrix}\end{split}\]

hence we can calculate \(\mathrm{d}{\bf S}\) here:

\[\begin{split}\mathrm{d}{\bf S} &= \left(\frac{\partial {\bf r}}{\partial \theta} \times \frac{\partial {\bf r}}{\partial \phi}\right)\,\mathrm{d}\theta\,\mathrm{d}\phi\\ &= R^2\begin{pmatrix} \cos(\theta)\cos(\phi) \\ \cos(\theta)\sin(\phi)\\ -\sin(\theta)\end{pmatrix} \times \begin{pmatrix} -\sin(\theta)\sin(\phi) \\ \sin(\theta)\cos(\phi)\\ 0 \end{pmatrix} \,\mathrm{d}\theta\,\mathrm{d}\phi\\ &= R^2 \begin{pmatrix} \sin^2(\theta) \cos(\phi) \\ \sin^2(\theta)\sin(\phi)\\ \sin(\theta) \cos(\theta)\end{pmatrix} \,\mathrm{d}\theta\,\mathrm{d}\phi \\ &= R^2 \begin{pmatrix} \sin(\theta) \cos(\phi) \\ \sin(\theta)\sin(\phi)\\ \cos(\theta)\end{pmatrix} \,\sin(\theta)\mathrm{d}\theta\,\mathrm{d}\phi \\\end{split}\]

We can then recall that the radial vector for spherical polar coordinates has the form:

\[\begin{split}\hat{\bf r} = \begin{pmatrix} \sin(\theta) \cos(\phi) \\ \sin(\theta)\sin(\phi)\\ \cos(\theta)\end{pmatrix}\end{split}\]

and therefore :

\[\mathrm{d}{\bf S} = R^2\,\sin(\theta)\,\mathrm{d}\theta\,\mathrm{d}\phi\,\hat{\bf r} \]

Thus the surface area integral takes the form:

\[A = \iint_A \mathrm{d}S = R^2 \int_0^{2\pi}\,\mathrm{d}\phi\,\int_0^\pi\,\sin(\theta)\,\mathrm{d}\theta = 2\pi R^2\Big[-\cos(\theta)\Big]_0^{\pi} = 4\pi R^2\]

Further worked examples:

1. Find the surface area for \(0 \leq x \leq 3\), \(0 \leq y \leq 3\) for a sphere:

\[x^2 + y^2 + z^2 = 9\]

We can try to solve this using Cartesian coordinates instead of polar here (spherical polar will also work though!) Lets try to apply \(z = f(x,\,y) = \sqrt{9 - x^2 - y^2}\),

\[\begin{split}\iint_A \mathrm{d}S &= \int_{-R}^R\,\mathrm{d}x\,\int_{-R}^R\,\mathrm{d}y\,\sqrt{\left(\frac{\partial z}{\partial x}\right)^2 + \left(\frac{\partial z}{\partial y}\right)^2 + 1} \\ &= \int_0^3\,\mathrm{d}x\,\int_0^3\,\mathrm{d}y\,\sqrt{ \frac{x}{\sqrt{9 - x^2 - y^2}} + \frac{y}{\sqrt{9 - x^2 - y^2}} + 1} \\ &= \int_0^3\,\mathrm{d}x\,\int_0^3\,\mathrm{d}y\,\frac{3}{\sqrt{9 - x^2 - y^2}}\end{split}\]

If we use a change of variable, \(x = \sqrt{9-y^2}\sin(\varphi) \Rightarrow \mathrm{d}x = \sqrt{9-y^2}\cos(\varphi)\,\mathrm{d}\varphi\) and therefore we have:

\[\iint_A \mathrm{d}S = 3\int_0^{\pi/2}\,\mathrm{d}\varphi \int_0^3 \,\mathrm{d}y = \frac{9\pi}{2}\]

which corresponds to \(\frac{1}{8}\) of the full sphere’s surface area \(36\pi\), as expected.

2. Find the surface area of a cone with height \(h\) and base radius \(R\).

Here we can use the parameterisation \(z,\, \theta\) to describe any point on this surface. This means we describe any point in cylindrical polar coordinates:

\[\begin{split}{\bf r} = \begin{pmatrix} \frac{R}{h}z\,\cos(\theta) \\ \frac{R}{h}z\,\sin(\theta) \\ z \end{pmatrix}\end{split}\]

with ranges \(0 \leq z \leq h\) and \(0 \leq \theta \leq 2\pi\). Then to find the vectors in terms of this parameterisation:

\[\begin{split}\frac{\partial {\bf r}}{\partial z} = \begin{pmatrix} \frac{R}{h}\,\cos(\theta) \\ \frac{R}{h}\,\sin(\theta) \\ 1 \end{pmatrix}\\ \frac{\partial {\bf r}}{\partial \theta} = \begin{pmatrix} -\frac{R}{h}z\,\sin(\theta) \\ \frac{R}{h}z\,\cos(\theta) \\ 0 \end{pmatrix}\end{split}\]

which means the integrand takes the form:

\[\begin{split}\frac{\partial {\bf r}}{\partial z} \times \frac{\partial {\bf r}}{\partial \theta} &= \begin{vmatrix} \hat{\bf x} & \hat{\bf y} & \hat{\bf z} \\ \frac{R}{h}\,\cos(\theta) & \frac{R}{h}\,\sin(\theta) & 1 \\ -\frac{R}{h}z\,\sin(\theta) & \frac{R}{h}z\,\cos(\theta) & 0 \end{vmatrix}\\ &= \begin{pmatrix} -\frac{R}{h}z\,\cos(\theta) \\ -\frac{R}{h}z\,\sin(\theta)\\ \frac{R^2}{h^2}z\end{pmatrix}\\ \Rightarrow \left|\frac{\partial {\bf r}}{\partial z} \times \frac{\partial {\bf r}}{\partial \theta}\right| &= \sqrt{\frac{R ^2}{h^2}z^2 + \frac{R^4}{h^4}z^2} = \frac{R}{h}z\sqrt{1 + \frac{R^2}{h^2}}\end{split}\]

and so integrating we find:

\[\begin{split}\iint_S\,\mathrm{d}S &= \int_0^{2\pi}\mathrm{d}\theta\,\int_0^h \frac{R}{h}z\sqrt{1 + \frac{R^2}{h^2}} \,\mathrm{d}z\\ &= 2\pi\frac{R}{h}\sqrt{1 + \frac{R^2}{h^2}}\Big[\frac{1}{2}z^2 \Big]_0^h = 2\pi\frac{R}{h}\frac{h^2}{2}\sqrt{1 + \frac{R^2}{h^2}} = \pi R\sqrt{h^2 + R^2}\end{split}\]