Contents

NSCI0007 Exam

Exam Start: N/A
Exam End: N/A

Instructions

  • At the exam end time, a copy of the exam folder NSCI0007_EXAM will be automatically taken for marking. Only files in this folder will be marked.

  • Enter your answers in the file answers.ipynb in the exam folder.

  • Any changes made to files made after the end time will not be marked.

  • This exam is open book. Candidates may refer to course notes, tutorials and any online materials.

  • Candidates may not confer with any other person during the exam period.

Introduction

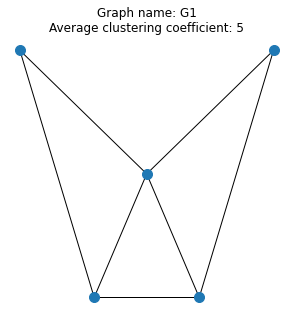
A graph is a collection of nodes connected by edges. The graph \(G_1\) below has 5 nodes and 7 edges:

G1

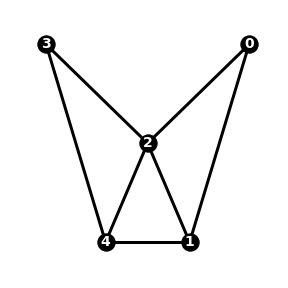
The adjacency matrix of a graph with \(n\) nodes is an \(n\) by \(n\) array, where the element in position \(i, j\) is 1 if node \(i\) is connected to node \(j\) by an edge, otherwise 0. The adjacency matrix of the graph \(G_1\) is:

\[\begin{split} \begin{bmatrix} 0 & 1 & 1 & 0 & 0\\ 1 & 0 & 1 & 0 & 1\\ 1 & 1 & 0 & 1 & 1\\ 0 & 0 & 1 & 0 & 1\\ 0 & 1 & 1 & 1 & 0\\ \end{bmatrix} \end{split}\]

In Python, this can be represented as a numpy array:

import numpy as np
G_1 = np.array([[0, 1, 1, 0, 0],
                [1, 0, 1, 0, 1],
                [1, 1, 0, 1, 1],
                [0, 0, 1, 0, 1],
                [0, 1, 1, 1, 0]])

Question 1 [4]

The neighbours of a node \(i\) are the nodes directly connected to node \(i\) by an edge. For example, in graph \(G_1\) the neighbours of node 0 are nodes 1 and 2.

Write a function neighbours(A, i) which, given an adjacency matrix A and node index i returns a list of neighbours of node i.

Test it with the code below:

import numpy as np
G_1 = np.array([[0, 1, 1, 0, 0],
                [1, 0, 1, 0, 1],
                [1, 1, 0, 1, 1],
                [0, 0, 1, 0, 1],
                [0, 1, 1, 1, 0]])
              
neighbours(G_1, 0)

[1, 2] # or [2, 1]

Question 2 [5]

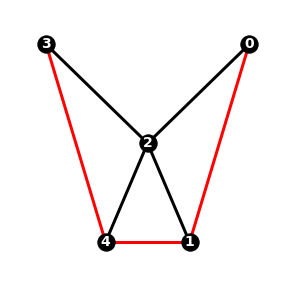
The clustering coefficient of a node measures how densely connected the node’s neighbours are. If the node has fewer than 2 neighbours then its clustering coefficient is zero, otherwise it is defined as follows:

\[\gamma(i) = m/(n^2−n)\]

where \(n\) is the number of neighbouring nodes and \(m\) is the number of edges between neighbouring nodes.

In \(G_1\), node 2 has 4 neighbours connected by 3 edges (coloured red in the figure below), so \(\gamma(2) = 3 / (4^2 - 4) = 3/12 = 1/4\).

G1

Write a function clustering_coefficient(A, i) which returns the clustering coefficient of node i, and test it using the code below:

clustering_coefficient(G_1, 2)

0.25

Question 3 [5]

A path is a sequence of nodes, where each node is connected to the next by an edge and no node is repeated. For example [0, 2, 1, 4] is a path in the graph \(G_1\), but [0, 1, 2, 0] and [0, 3, 4] are not.

Given a list nodes and graph with adjacency matrix A, write a function is_path(A, nodes) which returns True if nodes is a path in the graph, and otherwise returns False. Test your function with the three lists [0, 2, 1, 4], [0, 1, 2, 0] and [0, 3, 4].

Question 4 [4]

The average clustering coefficient of a graph is defined as the sum of the clustering coefficients of all nodes in the graph, divided by the number of nodes in the graph.

Write a function average_clustering_coefficient(A) and test the function against the graph \(G_1\).

Question 5 [4]

The Python library networkx can be used to analyse and plot graphs. Import the library, and use it to create a graph of \(G_1\). Plot the graph using the function networkx.draw.

https://networkx.org/documentation/networkx-1.7/tutorial/tutorial.html

Question 6 [8]

Each of the three files graphXX.txt contains the definition of a graph. Each file is structured as follows:

  1. graph name

  2. number of nodes

  3. The adjacency matrix, with one line per row

Write a script which reads the data from each file and generates a figure containing a plot of the graph annotated with the name and average clustering coefficient. Your three plots should look similar to the example below.

G1