Further Practice
3.5. Further Practice#
Exercise 3.13
A solid of revolution is a three-dimensional figure contstructed by rotating a curve about a straight line. We can estimate the volume of a solid of revolution by dividing it into a sequence of stacked discs and summing the volume of each.
A sphere of radius \(R\) is formed by rotating the curve \(y = \sqrt{R^2 - x^2}\) around the x-axis between \(-R\) and \(R\).
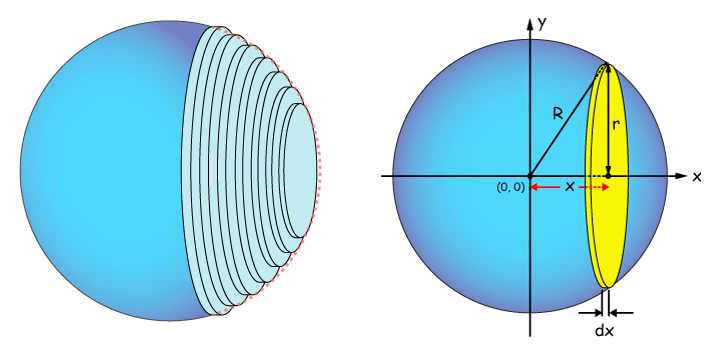
Use the following steps to estimate the volume of a sphere of radius 1.
Write a function
vol_disc(R, x, dx)which returns the volume of the disc centred at positionxwith thicknessdx.Estimate the volume of a sphere of radius 1 by dividing the figure into 10 discs equally spaced between
-1and1[use a value of 3.14159 for \(\pi\)].Write a function
sphere_vol(R, n)which returns the estimate of the volume of a sphere of radiusRcalculated by dividing it intondiscs.The estimate should get more accurate as we increase
n. We can estimate the accuracy by calculating the difference betweensphere_vol(R, n)andsphere_vol(R, n-1). ForR = 1, how large doesnneed to be so that difference between consecutive estimates is less than \(10^{-4}\)?
Exercise 3.14
In this question you will investigate the number of prime numbers below a number \(n\) (recall a prime number is a number divisible only by 1 and itself).
You will need to use Boolean variables which are variables that take the logical values True or False. For example, the following function divisible_by_two returns the Boolean value True if its argument is divisible two, and False otherwise.
def divisible_by_two(n):
if n % 2 == 0:
return True
else:
return False
k = 5
if divisible_by_two(k):
print(k, "is even")
else:
print(k, "is odd")
Write a function
is_divisible(n, m)which returnsTrueifnis divisible bym, and otherwise returnsFalse.Write a function
is_prime(n)which returnsFalseifnis divisible by any integer between2andn-1, and otherwise returnsTrue.Write a function
number_of_primes(n)which returns the number of prime numbers less than or equal ton[NB 1 is not a prime number].Draw a graph with
non the x-axis and the number of primes less than or equal tonon the y-axis.

