7. Isomorphic Graphs

We say that two graphs are isomorphic if they have the same network structure. Graphs $G_1$ and $G_2$ are isomorphic if there exists a matching between their nodes such that two nodes are connected by an edge in $G_1$ if and only if their corresponding nodes are connected by an edge in $G_2$.

Definition

An isomorphsim between two graphs $(V_1,E_1)$ and $(V_2,E_2)$ is a bijection (one-to-one correspondence)

$$f:V_1\to V_2$$

such that $(v_1,v_2)$ is in $E_1$ if and only if $(f(v_1),f(v_2))$ is in $E_2$.

If an isomorphism exists between two graphs, we say that the graphs are isomorphic.

7.1. Example

Find an isomorphism between the following two graphs.

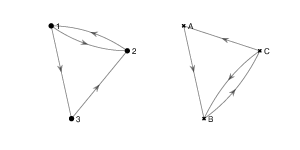
Solution

These two graphs are isomorphic under the isomorphism $f:\{1,2,3\}\to \{A,B,C\}$ where $f(1)=C,f(2)=B$ and $f(3)=A$.

7.2. Question 1

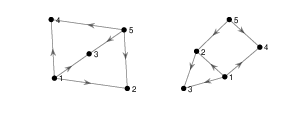
1. Find an isomorphism between the following two directed graphs:

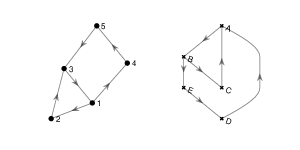
2. Find a subgraph of the egg-laying circuit isomorphic to the directed graph below.

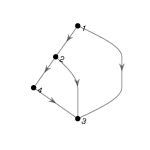
3. Use NetworkX functions subgraph and is_isomorphic to confirm your answer to 2.

7.3. Example

How many simple directed graphs are there with 3 nodes and two edges?

Solution

There are 4. Any other simple directed digraph with 3 nodes and 2 edges is isomorphic to one of these.

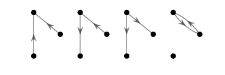
7.4. Question 2

Draw all simple directed graphs with 3 nodes and 3 edges.

7.4.1. Isomorphism from Adjacency Matrix

Given two graphs $G_1$ and $G_2$, we can check whether they are isomorphic by calculating the adjacency matrix of every permutation of the nodes of $G_1$. If one of them is equal to the adjacency matrix of $G_2$, then the two graphs are isomorphic.

There are $n!$ permutations of $n$ nodes, so even for relatively small graphs, checking for isomorphism can take a long time. There are $2.4\times {10}^{24}$ possible permutations of a graph with 20 nodes.

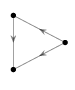
7.5. Question 3

Write down all $3!=6$ adjacency matrices of the following digraph.

7.6. Graph Invariants

Fortunately, the problem of checking whether two graphs are not isomorphic is often easier. For example, if $G_1$ has 5 nodes and $G_2$ has 6 nodes, they certainly are not isomorphic. A graph property which is preserved by isomorphism is called a graph invariant.

Some examples of graph invariants:

1. Number of nodes

2. Number of edges

3. Maximum node degree

4. Number of triangle (3-cycle) subgraphs

5. Number of connected components

7.7. Question

1. Show that the following pairs of graphs are not isomorphic by finding an invariant that they do not share.

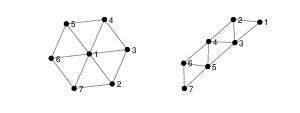
2. Write down two more graph invariants.