3.1. Exercises

Solution to Exercise 3.1

1.

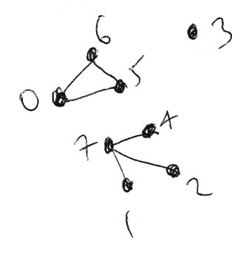
The connected components are \([1, 2, 4, 7]\), \([0, 5, 6]\) and \([3]\).

# 2.
def bfs(adj, i):
    visited = [i]
    frontier = [i]

    while len(frontier) > 0:
        next = frontier
        frontier = []
        for j in next:
            neighbours = adj[j]
            for k in neighbours:
                if not k in visited:
                    frontier.append(k)
                    visited.append(k)
    return visited

g = [[5, 6], [7], [7], [], [7], [0, 6], [0, 5], [1, 2, 4]]

for i in range(len(g)):
    print(bfs(g, i))

# 3.

import numpy as np

def path_distances(adj, i):
    visited = [i]
    frontier = [i]
    distances = np.zeros(len(adj))
    distances[:] = -1
    distances[i] = 0
    d = 0
    while len(frontier) > 0:
        d += 1
        next = frontier
        frontier = []
        for j in next:
            neighbours = adj[j]
            for k in neighbours:
                if not k in visited:
                    frontier.append(k)
                    visited.append(k)
                    distances[k] = d
    return distances

n = len(g)
d = np.zeros((n,n))
for i in range(n):
    d[i,:] = path_distances(g, i)

print(d)

[0, 5, 6]
[1, 7, 2, 4]
[2, 7, 1, 4]
[3]
[4, 7, 1, 2]
[5, 0, 6]
[6, 0, 5]
[7, 1, 2, 4]
[[ 0. -1. -1. -1. -1.  1.  1. -1.]
 [-1.  0.  2. -1.  2. -1. -1.  1.]
 [-1.  2.  0. -1.  2. -1. -1.  1.]
 [-1. -1. -1.  0. -1. -1. -1. -1.]
 [-1.  2.  2. -1.  0. -1. -1.  1.]
 [ 1. -1. -1. -1. -1.  0.  1. -1.]
 [ 1. -1. -1. -1. -1.  1.  0. -1.]
 [-1.  1.  1. -1.  1. -1. -1.  0.]]

Solution to Exercise 3.2

# 1.

g = [[3], [], [1, 4], [2], [8], [4], [4, 5], [6, 9], [3, 6, 10], [8], []]

# 2.

def print_length_2_walks(adj, i):
    for j in adj[i]:
        for k in adj[j]:
            print(i, j, k)

print("length 2 walks:")               
print_length_2_walks(g, 8)

# 3.

def print_length_2_paths(adj, i):
    for j in adj[i]:
        if i != j:
            for k in adj[j]:
                if i!=k and j!= k:
                    print(i, j, k)

print("length 2 paths:")            
print_length_2_paths(g, 8)

length 2 walks:
8 3 2
8 6 4
8 6 5
length 2 paths:
8 3 2
8 6 4
8 6 5