Answers
1.7. Answers#
Solution to Exercise 1.1
\([1,6],[6,1],[3,1],[3,4],[6,4],[4,4],[3,2],[4,2],[4,5],[2,5]\) (in any order)
\([6],[5],[1,4,2],[4,2,5],[],[1,4]\)
Solution to Exercise 1.2
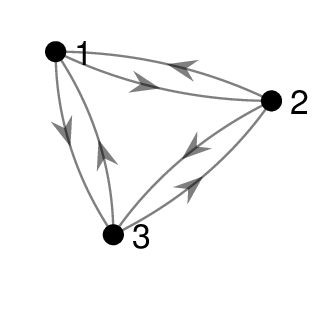
1) and 2)
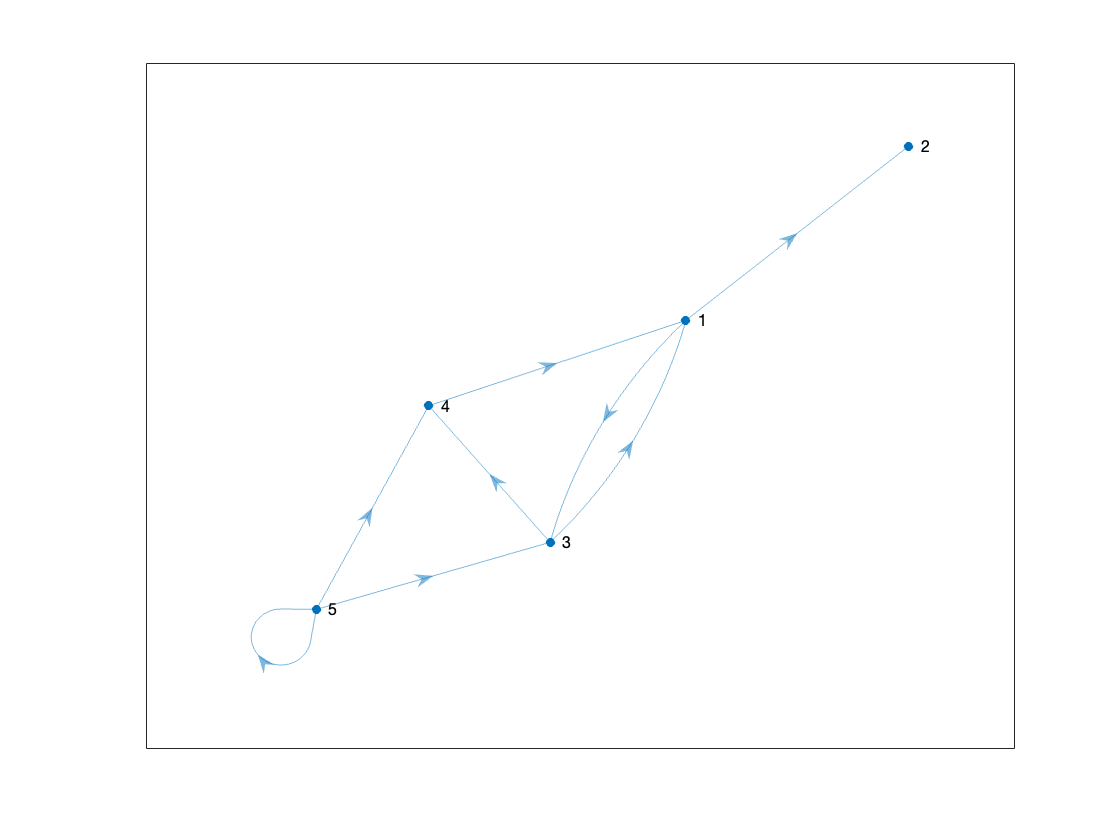
3)
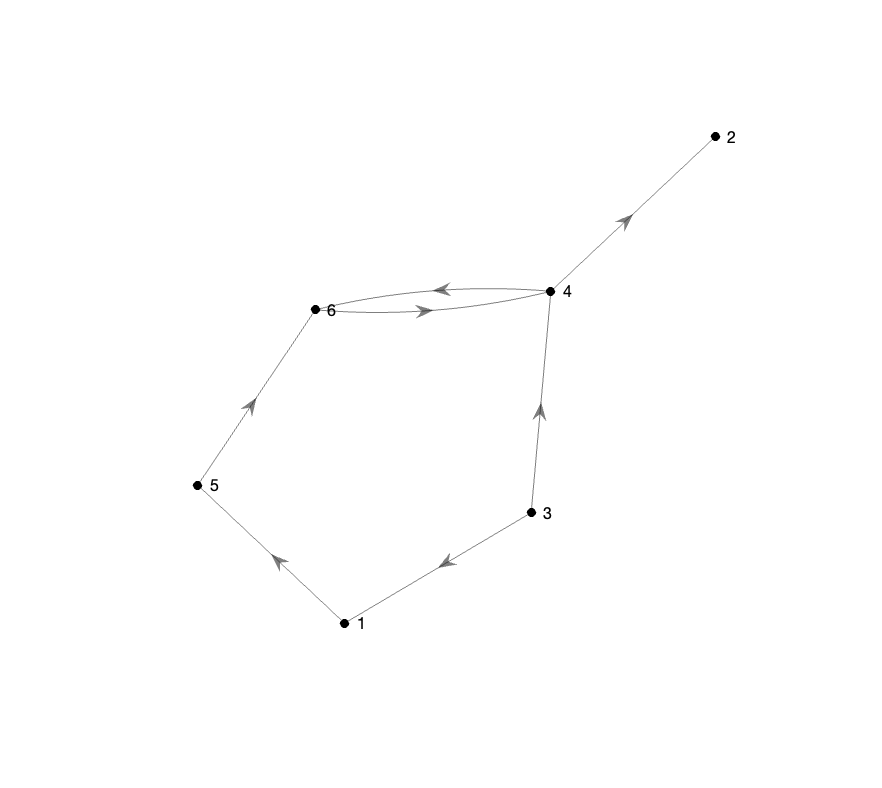
Solution to Exercise 1.3
1. There are 3 choices for the first node, and 2 choices for each of the 10 subsequent nodes. The total number of walks is therefore \(3 × 2^{10}\).
2. Paths from node 6 to node 4: \([6,4],[6,7,4],[6,7,3,4],[6,7,3,5,4]\). Paths from node 4 to node 6: none.
3. \([2,1,3,7,6,4]\).
Solution to Exercise 1.5
BFS starting at node 2:\([2,1,4,3,5,7,6]\)
Path distances from node 2: \(d = [1,0,2,1,3,4,3]\) where \(d(i)\) is the distance from node \(i\).BFS starting at node 6: \([6, 4, 7, 3, 5]\)
Path distances from node 6: \(d = [inf, inf, 2, 1, 3, 0, 1]\)
Question 7
1.
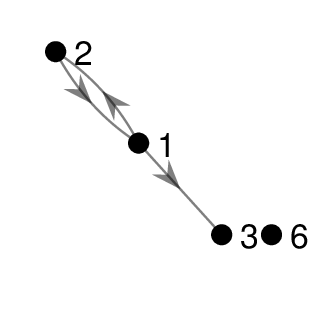
2. For node order 1, 2, 3, 6:
Solution to Exercise 1.6
Connected components: \([1, 5, 6, 7, 9], [4, 8], [2, 3, 10]\)