12. Doppler Shift#

The observation of wave behaviour can be affected when at least one of the wave source and/or wave observer are in relative motion. An example of this is shown in Fig. 12.1, where an ambulance siren is seen moving past an observer.

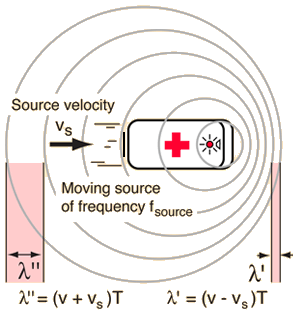
../_images/DopplerShiftAmbulance.png

Fig. 12.1 Effects on sound emitted by a moving source (here an ambulances siren) depending on whether the source is approaching \(\lambda''\) towards or receding \(\lambda'\) from an observer.#

We start with a source frequency/time period \(f_{source} = 1/T_{source}\), source wavelength of \(\lambda_{source}\), wave velocity in the transmission medium \(v\) and source velocity of \(v_s\) with respect to the observer.

Depending on how this relative motion is set up, we can

  • Wave source receding from an observer,

Since the source is receding from the observer, subsequent wavefronts get further apart, so the difference in observed wavelength grows each cycle by an additional factor:

\[\begin{split}\lambda'' &=& \left(v + v_s\right)T_{source} \\ \Rightarrow \lambda'' &=& \left(\frac{v + v_s}{v}\right) \lambda_{source} \\ \lambda'' = \frac{v}{f''} &=& \left(\frac{v + v_s}{f_{source}}\right) \\ \Rightarrow f'' &=& \left(\frac{v}{v + v_s}\right) f_{source}\end{split}\]

  • Wave source approaching an observer,

Since the source is approaching the observer, subsequent wavefronts get closer together, so the difference in observed wavelength shrinks each cycle by an additional factor:

\[\begin{split}\lambda' &=& \left(v-v_s\right)T_{source} \\ \Rightarrow \lambda' &=& \left(\frac{v - v_s}{v}\right) \lambda_{source} \\ \lambda' = \frac{v}{f'} &=& \left(\frac{v-v_s}{f_{source}}\right) \\ \Rightarrow f' &=& \left(\frac{v}{v-v_s}\right) f_{source}\end{split}\]

We may find that if the observer is also in relative motion with respect to the medium, with velocity \(v_o\) in same linear direction as \(v_s\), then these expressions may be modified taking the form:

\[\begin{split}f' = \left(\frac{v - v_o}{v - v_s}\right)f_{source} &\Longleftrightarrow& \lambda' = \left(\frac{v - v_s}{v - v_o}\right)\lambda_{source}\\ f'' = \left(\frac{v + v_o}{v + v_s}\right)f_{source} &\Longleftrightarrow& \lambda'' = \left(\frac{v + v_s}{v + v_o}\right)\lambda_{source}\end{split}\]

and variations can be found if \(v_0\) and \(v_s\) are in opposite directions.