4. Longitudinal Waves

4.1. Derivation from masses and springs

Lets start with the classic derivation of waves propagating, with a collection of \(N\) masses \(m\) connected together on springs (with spring constant \(k\)), each with equilibrium separation \(h\), as shown in Fig. 4.1. We can measure the horizontal displacement \(u(x,t)\) from the equilibrium positions.

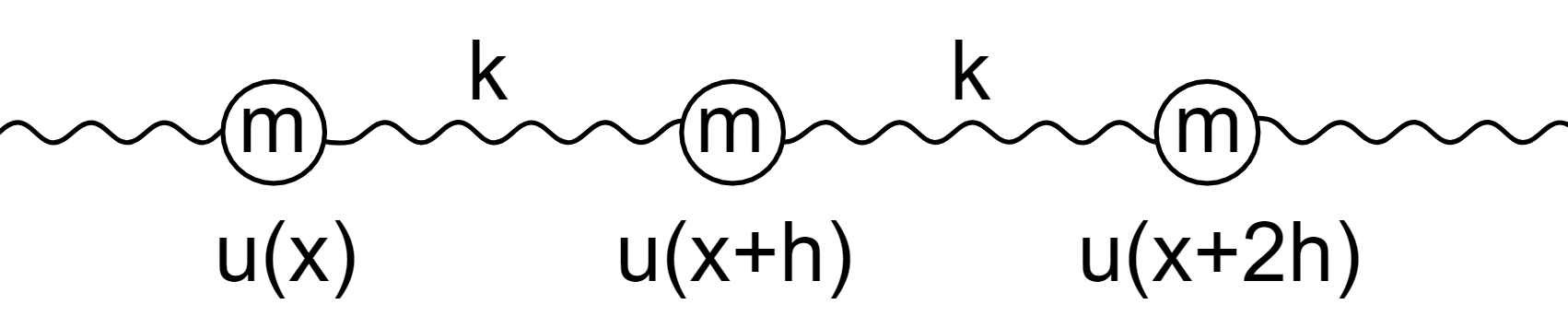
Fig. 4.1 Identical masses connected by identical springs.

If the springs follow Hooke’s law, then \(F_{H} = k\,u(x,t) \) and equally all the masses will follow Newton’s second law \(F_{N} = m \,a(x,t)\). We can analyse the dynamics of the middle mass, where the Hooke’s law forces will from both the spring \(x+h \rightarrow x+2h\) as well as the spring \(x \rightarrow x+h\)

\[\begin{split}F_N &= m \frac{\partial^2}{\partial t^2}u(x+h,t)\\ F_H &= k[u(x+2h,t) - u(x+h,t)] - k[u(x+h,t) - u(x,t)] \\ &= k[u(x+2h,t) - 2u(x+h,t) + u(x,t)]\end{split}\]

Since these defintions are equal, then by rearrangement:

(4.1)\[\frac{\partial^2}{\partial t^2}u(x+h,t) = \frac{k}{m}[u(x+2h,t) - 2u(x+h,t) + u(x,t)] \]

Lets also consider a chain of springs in series, as shown in Fig. 4.2

Fig. 4.2 Two springs in series with a mass

We can consider the total displacement of the mass \(m\), as well as as the individual springs displacements

\[\begin{split}F_{tot} &= k_{tot}\,x_{tot}\\ F_1 &= k_1\,x_1\\ F_2 &= k_2\,x_2\end{split}\]

If \(x_{tot}\) can be broken up into the individual springs displacements \(x_{tot} = x_1 + x_2\) then we simplify to:

\[F_{tot} = k_{tot}(x_1 + x_2)\]

by rearrangement this reduces to

\[\frac{F_{tot}}{k_{tot}} = \left(\frac{F_1}{k_1} + \frac{F_2}{k_2}\right)\]

Since the springs propagate the force applied through them, all the forces are the same \(F_{tot} = F_1 = F_2\), so we are finally left with:

\[\frac{1}{k_{tot}} = \frac{1}{k_1} + \frac{1}{k_2}\]

and therefore for two springs, the effective spring constant is:

\[k_{tot} = \left(\frac{1}{k_1} + \frac{1}{k_2}\right)^{-1}\]

If there are \(N\) springs in series, then this result takes the form:

\[\frac{1}{k_{tot}} = \frac{1}{k_1} + \frac{1}{k_2} + \dots + \frac{1}{k_N}\]

and if the springs are identical, \(k_1 = k_2 = \dots = k_N = k\) this result reduces to:

(4.2)\[\frac{1}{k_{tot}} = \frac{N}{k} \Rightarrow k_{tot} = \frac{k}{N}\]

We can substitute (4.2) into Equation (4.1):

\[\frac{\partial^2}{\partial t^2}u(x+h,t) = \frac{N\,k_{tot}}{m} [u(x+2h,t) - 2u(x+h,t) + u(x,t)]\]

Now if we want to consider the whole chain of masses and springs, then with \(N\) masses and total mass on the chain is \(m_{tot} = Nm\), which results in

\[\frac{\partial^2}{\partial t^2}u(x+h,t) = \frac{N^2\,k_{tot}}{m_{tot}} [u(x+2h,t) - 2u(x+h,t) + u(x,t)]\]

and if the the total chain length is \(L = Nh \Rightarrow N = \frac{L}{h}\), then:

(4.3)\[\Rightarrow \frac{\partial^2}{\partial t^2}u(x+h,t) = \frac{L^2\,k_{tot}}{m_{tot}} \frac{u(x+2h,t) - 2u(x+h,t) + u(x,t)}{h^2} \]

By taking the limit \(N \rightarrow \infty\) and therefore \(h \rightarrow 0\) for a finite chain length \(L\), this has exactly the form of the partial derivative in Equation (2.2). Hence Equation (4.3) has the form:

\[\frac{\partial^2}{\partial t^2}u(x,t) = \frac{L^2\,k_{tot}}{m_{tot}} \frac{\partial^2}{\partial x^2} u(x,t)\]

If we examine the units of the constants here:

\[\frac{[L]^2\,[k]}{[m]} = \frac{m^2\,N\,m^{-1}}{kg} = \frac{m^2\,kg\,m\,s^{-2}\,m^{-1}}{kg} = m^2\,s^{-2} = [v]^2\]

This results in the well known form of the wave equation in one dimension:

(4.4)\[\frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2} \]

where \(c\) is the wave speed of some form (more on this later).

4.2. Derivation from pressure waves

A common place to see longitundinal waves is in the case of pressure waves in fluids and gases - including in the air around us, which we use to send sounds and communicate in. The derivation is fairly similar to the one for masses and springs, although it relies much more on a continum hypthesis, we assume the medium that the pressure waves are set up in is homogeneous.