Chapter 4 exercise

Question 1

Using the eulerf function that was defined in the notes:

def dxdt(t,x):
    return -x+np.exp(-(t-2))

t,x = eulerf(dxdt,1,[0,10])
plt.plot(t,x)
plt.show()

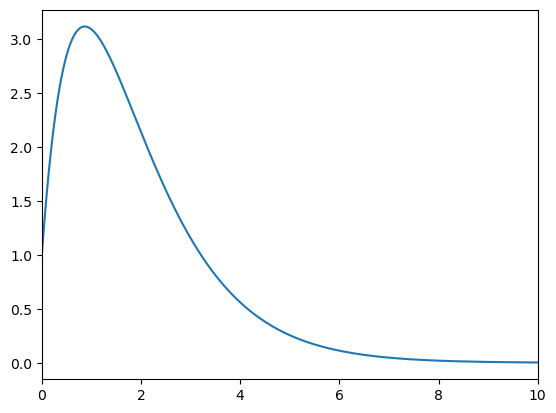
If you wish to compare, the analytic solution is given by

\[\begin{equation*} x=t e^{-(t-2)}+e^{-t} \end{equation*}\]

Question 2

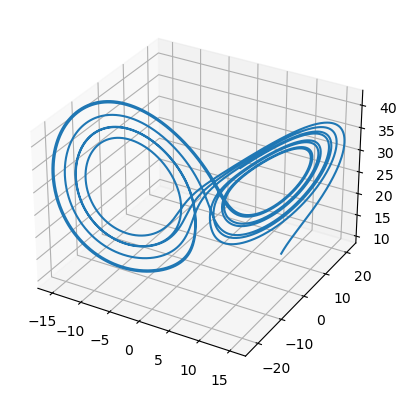
def dxdt(t,X,p,s,b):
    x,y,z=X
    dxdt=s*(y-x)
    dydt=x*(p-z)-y
    dzdt=x*y-b*z
    return np.array([dxdt,dydt,dzdt])

X0=[10,10,10]
t,X = eulerf(dxdt,X0,[0,10],p=28,s=10,b=2.667)

x,y,z=X.T #Extract the columns as variables

ax = plt.figure().add_subplot(projection='3d')
ax.plot(x, y, z)
plt.show()

Question 3

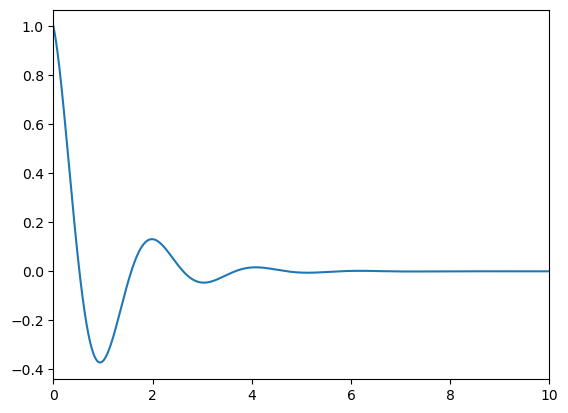
def dxdt(t,X):
    x,y=X
    dxdt=y
    dydt=-2*y-10*x
    return np.array([dxdt,dydt])

X0=[1,-1]
t,X = eulerf(dxdt,X0,[0,10])

plt.plot(t,X[:,0])
plt.show()