17. Composing Linear Functions#

17.1. The identity matrix#

The identity matrix \(I_n\) is the unique \((n \times n)\) matrix which has the property

\[I_n x = x \]

for any \(x \in \mathbb{R}^n\).

The identity matrix transforms the vector \(x\) to itself. It plays the same role in matrix multiplication as the number 1 does for multiplication of real numbers.

Definition

The identity matrix

\[\begin{split}I_n = \begin{pmatrix}1 & 0 & \cdots & 0\\0 & 1 & \cdots & 0\\\vdots & \vdots & \ddots & \vdots\\0& 0 & \cdots & 1\end{pmatrix}.\end{split}\]

We usually drop the subscript \(n\) when working with the identity matrix, because the order can be inferred.

Exercise 17.1

  1. Calculate \(I\begin{pmatrix}1 & 2\\3 & 4\end{pmatrix}\) and \(\begin{pmatrix}1 & 2\\3 & 4\end{pmatrix}I\).

  2. Use the identify matrix to factorise \(AB+\lambda B\) where \(\lambda\) is a scalar and \(A,B\) are square matrices.

17.2. Composition of Linear Transformations#

Given two linear transformations \(T:\mathbb{R}^n\rightarrow\mathbb{R}^m\) and \(U:\mathbb{R}^p\rightarrow\mathbb{R}^n\), the function \(T \circ U:\mathbb{R}^p\rightarrow\mathbb{R}^m\) is the composition of the two functions. That is, the function corresponding to applying first the function \(U\), then the function \(T\).

\[(T\circ U)(x) = T(U(x))\]

If \(T\) and \(U\) are linear transformations with matrices \(A\) and \(B\) respectively, then the product matrix \(AB\) represents the composition function \((T\circ U)\).

For example, suppose matrices \(A\) and \(B\) represent reflection in the \(y\)- and \(x\)-axis respectively:

\[\begin{split}A = \begin{pmatrix}-1 &0\\0&1\end{pmatrix}, \quad B = \begin{pmatrix}1 &0\\0&-1\end{pmatrix}.\end{split}\]

Then the matrix \(AB\) represents a rotation by \(\pi\) around the origin:

\[\begin{split}AB = \begin{pmatrix}-1 &0\\0&1\end{pmatrix}\begin{pmatrix}1 &0\\0&-1\end{pmatrix}=\begin{pmatrix}-1 &0\\0&-1\end{pmatrix}.\end{split}\]

Example

In Exercise 15.3 we reflected a set of points in the line through the origin at angle \(\theta\) with the \(x\)-axis. An equivalent way to do this would be to rotate clockwise by angle \(\theta\), reflect in the line \(y=0\) and then rotate back!

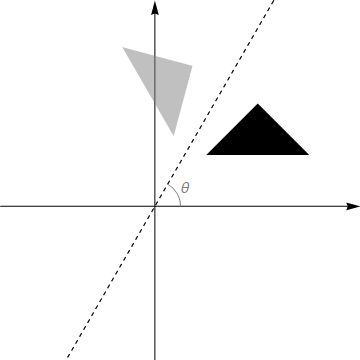
../../_images/three-step.png

Fig. 17.1 Reflection in a line as a three-step process. Equivalent to a reflection in the dashed line, we can 1) rotate clockwise by angle \(\theta\) 2) reflect in the horizontal axis 3) rotate anti-clockwise by angle \(\theta\).#

The transformation matrix for reflection in the line \(y=0\) is just \(\left(\begin{array}{cc}1 & 0 \\0 & -1 \\\end{array}\right)\), since \(x\mapsto x \), \(y\mapsto -y\).

Therefore, in matrix terms, we have

\[\begin{split} \begin{align*} A &= \begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix} \begin{pmatrix}1&0\\0&-1\end{pmatrix} \begin{pmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{pmatrix}\\ &= \begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix} \begin{pmatrix}\cos\theta&\sin\theta\\\sin\theta&-\cos\theta\end{pmatrix}\\ &= \begin{pmatrix}\cos 2\theta&\sin 2\theta\\\sin 2\theta&-\cos 2\theta\end{pmatrix} \end{align*} \end{split}\]

which is the result given previously.

Exercise 17.2

Use a composition of three matrix transformations to calculate the 2-d transformation matrix for a stretch, scale factor \(k\) parallel to the line \(y=\tan(\theta)x\).

17.3. Solutions#

Solution to Exercise 17.1

  1. \(I\begin{pmatrix}1 & 2\\3 & 4\end{pmatrix}=\begin{pmatrix}1 & 2\\3 & 4\end{pmatrix}I = \begin{pmatrix}1 & 2\\3 & 4\end{pmatrix}\).

  2. \(AB+\lambda B = (A+\lambda I)B\).

Solution to Exercise 17.2

We can describe this transformation as a rotation by \(\theta\) followed by a scale 2 stretch parallel to the \(x\)-axis followed by a rotation by \(-\theta\).

\[\begin{split} \begin{align*} A &=\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix}\begin{pmatrix}2&0\\0&1\end{pmatrix}\begin{pmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{pmatrix}\\ &=\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix}\begin{pmatrix}2\cos\theta&2\sin\theta\\-\sin\theta&\cos\theta\end{pmatrix}\\ &=\begin{pmatrix}k\cos^2\theta+\sin^2\theta & \frac{k-1}{2}\sin 2\theta\\\frac{k-1}{2}\sin 2\theta & k\cos^2\theta+\sin^2\theta\end{pmatrix} \end{align*} \end{split}\]