4.2. Modelling Space#
Recall that a numpy array is a data type used for storing a sequence of numerical values. The following code creates an array containing the values 5, 7, 4, 5:
import numpy as np
x = np.array([5, 7, 4, 5])
print(x)
[5 7 4 5]
The array x is a one-dimensional array since the elements are organised in a single row and a single index is required to access each element x[i].
Two-dimensional Arrays#
A two-dimensional array is similar to a one-dimensional array, but it can be visualised as a grid (or table) with rows and columns (Fig. 4.1).
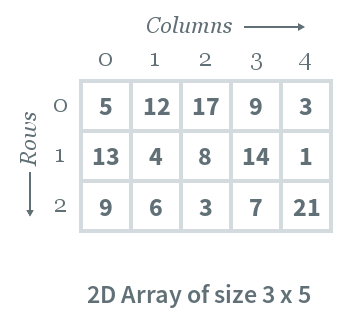
Fig. 4.1 A 2D array of size 3 by 5. The element at row \(i\) column \(j\) is accessed by x[i,j].#
We can create a two-dimensional array by nesting the rows in a second pair of square brackets. For example, to create the array in Fig. 4.1:
y = np.array([[5, 12, 17, 9, 3], [13, 4, 8, 14, 1], [9, 6, 3, 7, 21]])
print(y)
[[ 5 12 17 9 3]
[13 4 8 14 1]
[ 9 6 3 7 21]]
Note
Python allows us to split the code across several lines, which allows us to present the above code in a more readable way:
y = np.array([[5, 12, 17, 9, 3],
[13, 4, 8, 14, 1],
[9, 6, 3, 7, 21]])
We can access individual items by index using square brackets x[i, j] which represents the element in row i and column j. Recall that we number starting from zero so column 4 is the last column.
z = y[1, 4] # extract element at row 1 column 4
print(z)
1
Exercise 4.1
a = np.array([[1, 2, 3, 4], [5, 6, 7], [9, 10, 11, 12]])
Correct the code above so that it creates an array with 3 rows and 4 columns.
Then, change the element in the last row and column from 12 to 100.
Solution to Exercise 4.1
The second row only has 3 elements in, so we just need to add in the missing number. To change the element in the last row and column, remember that python starts counting from zero, so row 2 is the last row and column 3 is the last column.
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
a[2, 3] = 100
Slicing#
Use a colon : in place of a row or column index in order to extract an entire row or column from an array.
y = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# extract the top row of the array
top_row = y[0,:]
print(top_row)
[1 2 3]
left_column = y[:,0]
print(left_column)
[1 4 7]
Supply starting and ending indexes to extract parts of an array. Remember that in Python, the index i:j will extract all the entries from i up to and including j - 1.
left_two_columns = y[:,0:2]
print(left_two_columns)
[[1 2]
[4 5]
[7 8]]
See Fig. 4.2 for an illustration of slicing 2d arrays.
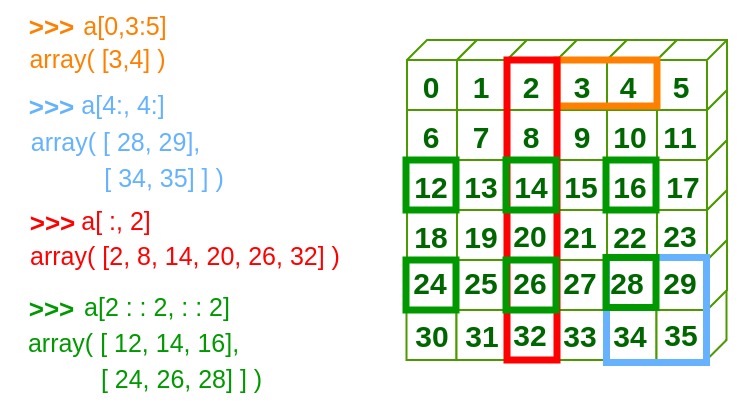
Fig. 4.2 Slicing a 2d array.#
Array functions#
To create a 2-dimensional array filled with zeros, use the function np.zeros((n, m)), where n is the number of rows and m is the number of columns. Note that we have to use two pairs of brackets in this case.
x = np.zeros((5, 5))
print(x)
[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
If we are given an array, but don’t know its dimensions, we can use the shape attribute:
z = np.array([[5, 8, 3, 2, 6, 6, 7, 4, 6, 4, 3, 7, 2, 3, 6, 7, 7], [5, 8, 3, 2, 6, 6, 7, 4, 6, 4, 3, 7, 2, 3, 6, 7, 7], [5, 8, 3, 2, 6, 6, 7, 4, 6, 4, 3, 7, 2, 3, 6, 7, 7], [5, 8, 3, 2, 6, 6, 7, 4, 6, 4, 3, 7, 2, 3, 6, 7, 7], [5, 8, 3, 2, 6, 6, 7, 4, 6, 4, 3, 7, 2, 3, 6, 7, 7], [5, 8, 3, 2, 6, 6, 7, 4, 6, 4, 3, 7, 2, 3, 6, 7, 7]])
n, m = z.shape
print("rows:", n)
print("cols:", m)
rows: 6
cols: 17
Other useful functions are np.max, np.min, np.sum and np.average which return the maximum, minimum, total and average value of the entire array.
print(np.sum(z))
516
Exercise 4.2
Determine the number of rows and columns of big_array, then calculate
The total of the last row
The average of the middle column
big_array = np.array([[4, 7, 2, 4, 6, 8, 5, 3, 2, 2, 3, 6, 4, 3, 4, 6, 8, 10, 3, 5, 0], [8, 2, 6, 5, 4, 4, 4, 4, 4, 4, 7, 5, 4, 3, 7, 5, 6, 4, 2, 3, 4], [1, 1, 1, 1, 3, 4, 3, 2, 3, 2, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 1], [3, 6, 2, 7, 2, 7, 2, 7, 2, 7, 2, 7, 2, 3, 5, 2, 6, 3, 5, 5, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]])
Solution to Exercise 4.2
To work out the number of rows and colums in big_array we can use shape:
n, m = big_array.shape
print("rows:", n)
print("cols:", m)
Then to find the total of the last row and the average of the middle column, we can use indexes to extract the relevant entries of the array and then use np.sum and np.average. There are 21 columns in total, so the elevent column is in the middle - but because python counts from 0, this is the column at index 10:
# last row is row n-1
print(np.sum(big_array[n-1, :]))
# middle column is at index 10
print(np.average(big_array[:, 10]))
Nested Loops#
For loops may be nested by placing one inside another. The following example repeats the inner loop 4 times for each pass through the outer loop, resulting in a total of 20 iterations.
Note that we must use distinct iterator variables i and j for the outer and inner loops.
for i in range(5):
for j in range(4):
print(i + j, end=" ")
print()
0 1 2 3
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7
Note
By default, the print function adds a newline character, which means that consecutive calls to print result in output on separate lines.
To avoid this, use print("text", end=" ").
Exercise 4.3
Use nested for loops to print the following patterns:
*
**
***
****
*****
-+-+-
+-+-+
-+-+-
+-+-+
-+-+-
(Hint: check if i + j is odd or even).
Solution to Exercise 4.3
The first pattern has five lines so the outer for loop should have 5 iterations. Then on line 1, we should print 1 star, 2 on line 2, 3 on line 3, and so on. In order to do this, we can use the iterator variable from the outer loop inside the range of the inner loop. Notice that range(0) is empty, so we need to set the upper limit of the inner iterator variable as one more than the outer iterator variable:
for i in range(5):
for j in range(i + 1):
print("*", end = "")
print()
The second pattern also has five lines, so the outer for loop should have five iterations. The pattern also has five columns so the inner for loop will also have five iterations. Following the hint, notice that if i+j is even, then i+j+1 and i+j-1 will be odd, and vice versa. So if we check whether i+j is even or odd and print a different character accordingly, we should get the pattern.
for i in range(5):
for j in range(5):
if (i + j) % 2 == 0:
# even
print("-", end = "")
else:
# odd
print("+", end = "")
print()
Creating and Building Arrays#
Arrays are fixed-size, which means that once created we can’t add extra elements. A common pattern when working with arrays is to firstly create an emtpy array of the ultimate size, then to gradually fill it with values.
Suppose we would like to create a 5 by 5 array whose elements are the sum of the row and column numbers. First, let’s create an empty array with 5 rows and 5 columns.
x = np.zeros((5, 5))
print(x)
[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
Next fill it with elements using two nested loops.
for i in range(5):
for j in range(5):
x[i, j] = i + j
print(x)
[[0. 1. 2. 3. 4.]
[1. 2. 3. 4. 5.]
[2. 3. 4. 5. 6.]
[3. 4. 5. 6. 7.]
[4. 5. 6. 7. 8.]]
Exercise 4.4
Use nested for loops to create arrays as follows:
[[1. 0. 0. 0. 0.]
[2. 2. 0. 0. 0.]
[3. 3. 3. 0. 0.]
[4. 4. 4. 4. 0.]
[5. 5. 5. 5. 5.]
[[1. 0. 1. 0. 1.]
[0. 1. 0. 1. 0.]
[1. 0. 1. 0. 1.]
[0. 1. 0. 1. 0.]
[1. 0. 1. 0. 1.]]
Solution to Exercise 4.4
We can start both arrays with an array containing zeros with 5 rows and 5 columns.
In the first array, the element at row i and column j takes the value i + 1 when j <= i and 0 otherwise. So to fill the array we can combine two nested for loops and an if statement:
a = np.zeros((5, 5))
for i in range(5):
for j in range(5):
if j <= i:
a[i, j] = i + 1
# we don't need an else here because all the other elements are already 0
print(a)
Similar to the pattern we printed in the last exercise, in the second array there is a 1 at row i column j when i+j is even, and a 0 when it is odd.
b = np.zeros((5, 5))
for i in range(5):
for j in range(5):
if (i + j) % 2 == 0:
# even
b[i, j] = 1
# we don't need an else here because all the other elements are already 0
print(b)
Vector Operations#
Arrays support vector operations. These allow us to perform operations on every item in the array simultaneously, without having to use a loop. For example, to add 10 to every element in an array:
y = x + 10
print(y)
[15 17 14 15]
Or to calculate the square of every element of the array:
z = x ** 2
print(z)
[25 49 16 25]
Note this is only possible because x is a numpy array. The following will not work:
a = [1, 2, 3]
b = a + 1 # error since a is a list
We can also perform vector operations on two arrays. For example, to multiply two arrays element-wise:
x = np.array([2, 4, 6, 8])
y = np.array([1, 3, 5, 7])
z = x * y # multiply two arrays element-by-element
print("x * y:", z)
x * y: [ 2 12 30 56]

