3.4. Exercises#

Exercise 3.13

Last week you used the following equations to model the dynamics of the Belousov–Zhabotinsky reaction where \(X_i\) and \(Y_i\) are the concentrations of the two reactants X (red) and Y (colourless) at timestep \(i\). Each timestep is one second.

\[\begin{split}\begin{align} X_{i+1} &= X_i + k_1-k_2X_i + k_3X_i^2Y_i\\ Y_{i+1} &= Y_i + k_4X_i - k_3X_i^2Y_i. \end{align}\end{split}\]

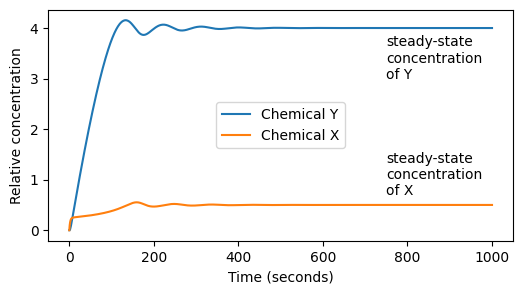
For the parameter values \(k_1=0.1\), \(k_2=0.4\), \(k_3=0.1\) and \(k_4=0.2\), the system results in decaying oscillations of the concentrations \(X\) and \(Y\). Over time the system reaches equilibrium and the values of \(X\) and \(Y\) reach a steady state. The figure below shows the results of the simultion with initial condtions \(X[0] = Y[0] = 0\).

1. Assuming the initial concentrations are zero, run the simulation with the parameters above for \(1000\) time steps. Plot \(X\) and \(Y\) on the same figure, as below.

2. Assuming that the system has reached a steady state after 1000 timesteps, we can define the steady-state concentrations to be \(X_{1000}\) and \(Y_{1000}\). Determine the steady-state values of \(X\) and \(Y\).

3. Write a function steady_state_X(k1, k2, k3, k4) which runs the simulation for the given values of \(k_1\), \(k_2\), \(k_3\) and \(k_4\), then returns the steady-state value of \(X\). Check that it gives the expected value for \(k_1=0.1\), \(k_2=0.4\), \(k_3=0.1\) and \(k_4=0.2\).

ss_x = steady_state_X(0.1, 0.4, 0.1, 0.2)
print(ss_x) # should print the expected value

4. Determine the steady-state value of X for \(k_1=0.1\), \(k_2=0.4\), \(k_3=0.1\) and a range of values of \(k_4\) between \(0\) and \(0.3\). Plot the results on a graph with \(k_4\) on the x-axis and the steady-state value of \(X\) on the y-axis.

5. Write a function max_X(k1, k2, k3, k4) which returns the peak value of the concentration of X, then (on the same graph as the previous question) plot the peak concentration of X for \(k_4\) between \(0\) and \(0.3\). (Use the numpy function np.max which returns the maximum value of an array).

../_images/af6feda6c833abf7d86f6f5507f022c7d8bb8d0288a6058b1d9af33f7f0d51b9.png

Exercise 3.14

In this question you will investigate the number of prime numbers below a number \(n\) (recall a prime number is a number divisible only by 1 and itself).

You will need to use Boolean variables which are variables that take the logical values True or False. For example, the following function divisible_by_two returns the Boolean value True if its argument is divisible two, and False otherwise.

def divisible_by_two(n):
    if n % 2 == 0:
        return True
    else:
        return False

k = 5
if divisible_by_two(k):
    print(k, "is even")
else:
    print(k, "is odd")

  1. Write a function is_divisible(n, m) which returns True if n is divisible by m, and otherwise returns False.

  2. Write a function is_prime(n) which returns False if n is divisible by any integer between 2 and n-1, and otherwise returns True.

  3. Write a function number_of_primes(n) which returns the number of prime numbers less than or equal to n [NB 1 is not a prime number].

  4. Draw a graph with n on the x-axis and the number of primes less than or equal to n on the y-axis.

Exercise 3.15

A solid of revolution is a three-dimensional figure contstructed by rotating a curve about a straight line. We can estimate the volume of a solid of revolution by dividing it into a sequence of stacked discs and summing the volume of each.

A sphere of radius \(R\) is formed by rotating the curve \(y = \sqrt{R^2 - x^2}\) around the x-axis between \(-R\) and \(R\).

a

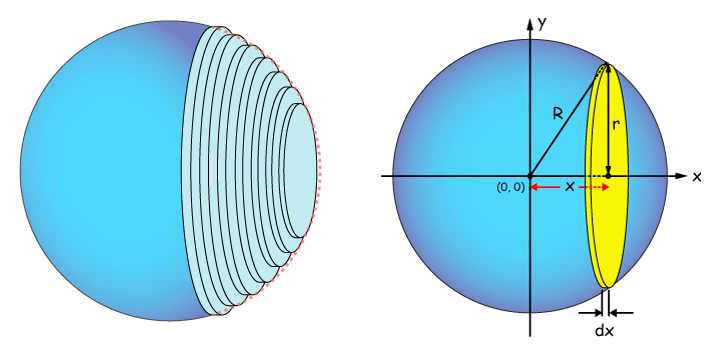
Use the following steps to estimate the volume of a sphere of radius 1.

  1. Write a function vol_disc(R, x, dx) which returns the volume of the disc centred at position x with thickness dx.

  2. Estimate the volume of a sphere of radius 1 by dividing the figure into 10 discs equally spaced between -1 and 1 [use a value of 3.14159 for \(\pi\)].

  3. Write a function sphere_vol(R, n) which returns the estimate of the volume of a sphere of radius R calculated by dividing it into n discs.

  4. The estimate should get more accurate as we increase n. We can estimate the accuracy by calculating the difference between sphere_vol(R, n) and sphere_vol(R, n-1). For R = 1, how large does n need to be so that difference between consecutive estimates is less than \(10^{-4}\)?