Solutions (3.13)

First, to run the simulation we can use the same approach as last week.

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt

# set up variables and arrays
n = 1001
k1 = 0.1
k2 = 0.4
k3 = 0.1
k4 = 0.2

X = np.zeros(n)
Y = np.zeros(n)

# initialise variables (not strictly necessary here!)
X[0] = 0
Y[0] = 0

# implement equations
for i in range(n - 1):
    X[i+1] = X[i] + k1 - k2*X[i] + k3*(X[i]**2)*Y[i]
    Y[i+1] = Y[i] + k4*X[i] - k3*(X[i]**2)*Y[i]

# plot on the same figure
plt.figure(figsize=(5,5))
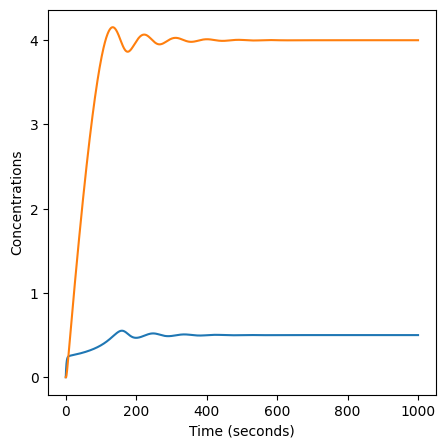
plt.plot(X)
plt.plot(Y)
plt.xlabel("Time (seconds)")
plt.ylabel("Concentrations")

Text(0, 0.5, 'Concentrations')

Determine the steady state

We are told that the system is in equilibrium after \(1000\) steps (and we can see from the figure that oscillations are not visible after about 600 steps), so to determine the steady state value of \(X\) we just need to check the value of \(X_{1000}\).

print('The steady state value of X is', X[1000])

The steady state value of X is 0.49999157908818176

Turning into a function

As we saw in the tutorial, we just need to wrap our existing code in a few extra lines to turn it into a function that can handle lots of values of \(k_4\).

def steady_state_X(k1, k2, k3, k4):
    # set up variables and arrays
    n = 1001

    X = np.zeros(n)
    Y = np.zeros(n)

    # initialise variables (not strictly necessary here!)
    X[0] = 0
    Y[0] = 0

    # implement equations
    for i in range(n - 1):
        X[i+1] = X[i] + k1 - k2*X[i] + k3*(X[i]**2)*Y[i]
        Y[i+1] = Y[i] + k4*X[i] - k3*(X[i]**2)*Y[i]
        
    #return the steady state
    return(X[1000])

To test this we can check it returns the same value as above for \(k_1=0.1\), \(k_2=0.4\), \(k_3=0.1\) and \(k_4=0.2\).

print("The steady state value of X is", steady_state_X(0.1, 0.4, 0.1, 0.2))

The steady state value of X is 0.49999157908818176

As we expected!

Explore behaviour for changing \(k_4\)

We would like to explore how the steady state value of \(X\) changes for values of \(k_4\) between \(0\) and \(0.3\). We did something similar in the tutorial, so we can modify our existing code:

# set up variables and arrays
k4_array = np.linspace(0, 0.3, 1000)
steady_state = np.zeros(1000) # be careful not to give this the same name as the function!

for i in range(1000):
    # Calculate the steady state value of X
    # for the given value of k_4
    steady_state[i] = steady_state_X(0.1, 0.4, 0.1, k4_array[i])

# Create a plot of steady state values against k_4 values
plt.figure(figsize=(4,4))
plt.plot(k4_array, steady_state)
plt.title('Steady state value against k_4')
plt.xlabel('k_4')
plt.ylabel('Steady state value')

Text(0, 0.5, 'Steady state value')

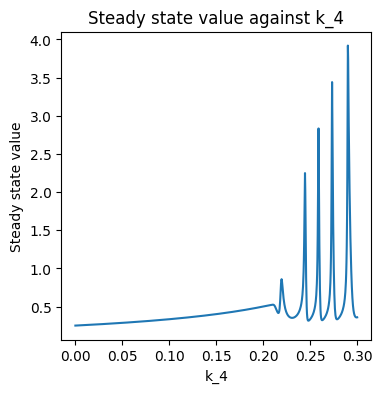
We can see that as \(k_4\) increases from \(0\) to \(0.2\), the steady state value also gradually increases. When \(k_4\) is larger than \(0.2\) the steady state value appears to oscillates rapidly. This is because for values of \(k_4\) above about \(0.2\), the system doesn’t reach a steady state.

def max_X(k1, k2, k3, k4):
    # set up variables and arrays
    n = 1001

    X = np.zeros(n)
    Y = np.zeros(n)

    # initialise variables (not strictly necessary here!)
    X[0] = 0
    Y[0] = 0

    # implement equations
    for i in range(n - 1):
        X[i+1] = X[i] + k1 - k2*X[i] + k3*(X[i]**2)*Y[i]
        Y[i+1] = Y[i] + k4*X[i] - k3*(X[i]**2)*Y[i]
        
    #return the steady state
    return(np.max(X))

# set up variables and arrays
k4_array = np.linspace(0, 0.3, 1000)
steady_state = np.zeros(1000) 
max_X_array = np.zeros(1000)

for i in range(1000):
    # Calculate the steady state value of X
    # for the given value of k_4
    steady_state[i] = steady_state_X(0.1, 0.4, 0.1, k4_array[i])
    max_X_array[i] = max_X(0.1, 0.4, 0.1, k4_array[i])

# Create a plot of steady state and max values against k_4 values
plt.figure(figsize=(4,4))
plt.plot(k4_array, steady_state, label="steady state")
plt.plot(k4_array, max_X_array, label="maximum")
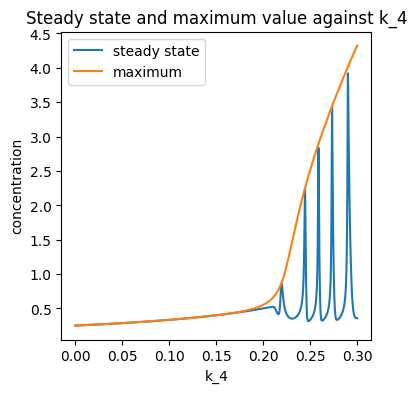
plt.title('Steady state and maximum value against k_4')
plt.xlabel('k_4')
plt.ylabel('concentration')
plt.legend()

<matplotlib.legend.Legend at 0x13d769f1848>