25. Limit cycles¶

Definition

A limit cycle is an isolated periodic solution, unlike a centre which has a family of periodic solutions.

For a stable limit cycle all trajectories approach the limit cycle as \(t\rightarrow\infty\)
For an unstable limit cycle all trajectories approach the limit cycle as \(t\rightarrow -\infty\)

A limit cycle can only exist in a nonlinear system. It occurs when the stabilising or destabilising effect of the nonlinear terms is opposite to that of the linear terms.

25.1. Example¶

By way of illustration, we consider the following problem

(25.1)¶\[\begin{align} \dot{x} &=x-y-x(x^2+y^2),\\ \dot{y} &=x+y-y(x^2+y^2). \end{align}\]

For this example it is instructive to transform to polar coordinates \(x=r\cos(\theta)\), \(y=r\sin(\theta)\), which gives the simpler-looking system

(25.2)¶\[\begin{align} \dot{r}&= r(1-r^2), \quad r\geq 0,\\ \dot{\theta}&=1. \end{align}\]

Solutions satisfying \(\dot{r}=0\) occur when \(r=0\) (point) and when \(r=1\) (cycle) as illustrated.

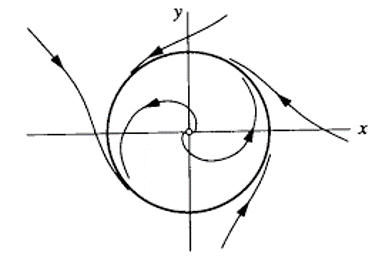
The stability of the cycle and equilibrium point can be inferred by noting that

\(\dot{r}>0\) for \(0<r<1\)
\(\dot{r}<0\) for \(r>1\).

Hence, the origin is unstable and the limit cycle is stable for this example.

Note

Limit cycles are generally not circular and must be found numerically. They can be extremely difficult to locate.

We have already seen illustrated examples of limit cycles in in Exercise 22.2 and Exercise 23.5. The systems we looked at in those exercises contained parameters and we saw that the limit cycle emerged for particular parameter regimes. This is another example of bifurcation behaviour.

25.2. Hopf bifurcation¶

A Hopf bifurcation occurs when a parameter in the system creates a change from a stable/unstable equilibrium point to an unstable/stable equilibrium point, together with a periodic solution that takes the form of a limit cycle.

Sub/supercritical

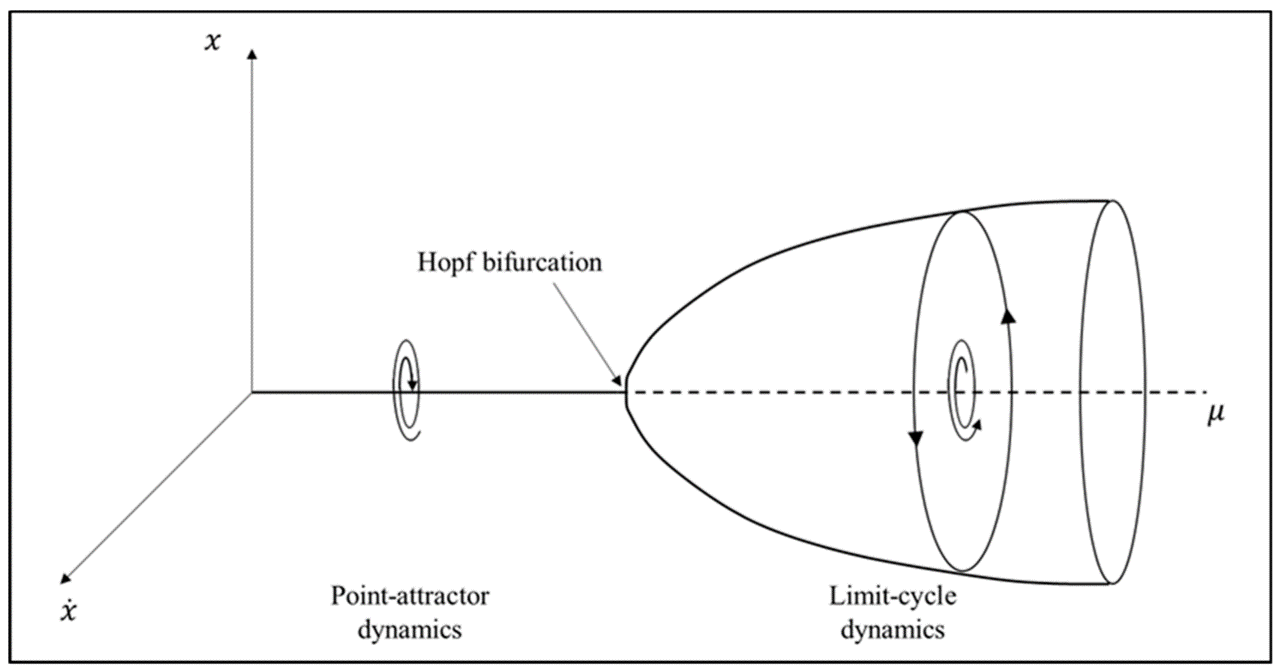
A Hopf bifurcation is said to be subcritical if the limit cycle is unstable and supercritical if the limit cycle is stable.

An illustration of a subcritical Hopf bifurcation is shown below. Here the bifurcation diagram has been shown in 3D to make it easier to infer what is happening. However, the normal representation of a bifurcation diagram is in 2D with only the extrema (max/min) values of the limit cycle indicated.

An example of how a subcritical bifurcation might be illustrated in 2D is shown below. The image is taken from a research paper investigating glucose-stimulated insulin secretion in the human pancreas, regulated by calcium concentration.

The horizontal axis shows the calcium concentration, which is varied as a parameter, and the vertical axis shows the equilibrium points and their stability. The max/min of the limit cycle are also shown.

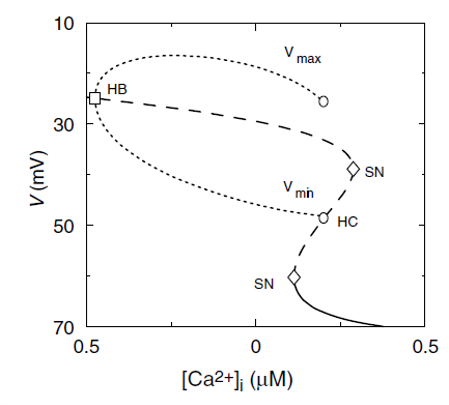
On the diagram the following notation is used:

HB: Hopf bifurcation
SN: Saddle node bifurcation
HC: Homoclinic bifurcation

At a homoclinic bifurcation a limit cycle collides with a saddle node. The limit cycle is annihilated. The details of homoclinic bifurcations are beyond the scope of this course.

Exercise 25.1

For the glycolysis problem introduced in Exercise 22.2, with \(k=v_0=1\), show that there is an equilibrium point at \((s,p)=(1/c,1)\). Find the eigenvalues and show that decreasing the parameter past \(c=1\) creates a Hopf bifurcation.

By referring back to the results illustrated in Exercise 22.2, say whether the Hopf bifurcation is supercritical or subcritical.

Let us take

\[\begin{align*} f(p,s)&=csp^2-kp,\\ g(p,s)&=v_0-csp^2. \end{align*}\]

The equilibrium point can be found by first setting \(g=0\), which gives \(csp^2=v_0\).

Substituting into \(f=0\) then provides

\[\begin{equation*} p=\frac{v_0}{k}, \qquad s=\frac{v_0}{cp^2}, \end{equation*}\]

and for the case where \(v_0=k=1\) we obtain \((s,p)=(1/c,1)\).

The Jacobian matrix, evaluated at the equilibrium point for \(v_0=k=1\) is

\[\begin{equation*} J=\begin{bmatrix}2csp-k & cp^2\\-2csp & -cp^2\end{bmatrix} \quad = \quad \begin{bmatrix}1& c\\-2& -c\end{bmatrix} \end{equation*}\]

The eigenvalues are found to be

\[\begin{equation*} \lambda = \frac{(1-c)\pm \sqrt{\theta}}{2}, \qquad \theta=c^2-6c+1 \end{equation*}\]

The quantity \(\theta\) is shown below. It is negative for \(3-2\sqrt{2}<c<3+2\sqrt{2}\). In this range, the solution trajectories near to the equilibrium point are spirals.

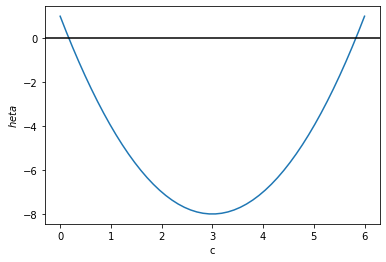
For \(3-2\sqrt{2}<c<1\) the spiral trajectories are unstable (positive real part).
For \(1<c<3+2\sqrt{2}\) the spiral trajectories are stable (negative real part).

The transition from an unstable to a stable spiral in a nonlinear system strongly hints at the possibility of a limit cycle in one of these two regimes.

To know where the limit cycle will occur is difficult without plotting some solution trajectories. We have done this in Exercise 22.2 and we found that the limit cycle appears in the region where the equilibrium point is unstable. Hence, the limit cycle is stable and this is an example of a supercritical Hopf bifurcation.

Side note:

It is possible to infer the stability of the limit cycle by transforming to a polar coordinate system with origin at the equilibrium point. Undertaking this level of investigation is beyond the scope of the course, but if you did it you would find that

\[\begin{equation*} \frac{\mathrm{d}r}{\mathrm{d}t}=\alpha r^2 + \beta r^3 +\gamma r^4 \end{equation*}\]

where the coefficients \(\alpha,\beta,\gamma\) depend on \(\theta\). When the distance from the equilibrium point is large, the term in \(r^4\) dominates. It’s coefficient is

\[\begin{equation*} \gamma = 2c\cos^2(\theta)(\cos(\theta)\sin(\theta)-\sin^2(\theta)) \end{equation*}\]

The average of \(\gamma\) over \(\theta\in[0,2\pi]\) is found to be negative, which suggests that the nonlinear terms have a stabilising effect.

Exercise 25.2

Find the eigenvalues of the Rayleigh problem introduced in Exercise 23.5. Show that a Hopf bifurcation occurs at \(c=0\). Is this a supercritical or a subcritical bifurcation?

Mathematics for Natural Sciences 2

Limit cycles

Contents

25. Limit cycles¶

25.1. Example¶

25.2. Hopf bifurcation¶