.md .pdf

Contents

2. Integration Preliminaries

2.1. Arc Length

Suppose that we have a function \(y = f(x)\), we know through integration that we can find the area under the curve, as shown in Fig. 2.1.

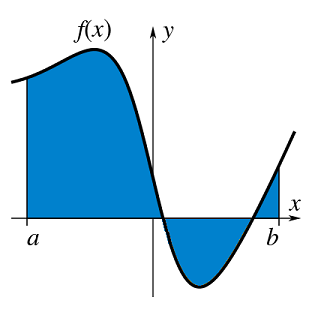
Fig. 2.1 The area (in blue) under a function \(f(x)\) over the interval \(x \in [a,\,b]\) given by the integral \(\int_a^bf(x)\,\mathrm(d)x\).

Another question that we could ask however is what is the length of the path traced out by the function \(f(x)\) over the range \([a,\,b]\), as shown in Fig. 2.2.

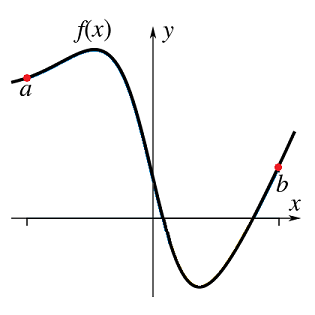
Fig. 2.2 The path traced out by the function \(f(x)\) over the interval \(x \in [a,\,b]\).

To find an expression for this length \(S\), we can break up the path into infinitesimal segments and then integrate these over the whole function. We can see this process in Fig. 2.3, where we break down the change in arc length \(\Delta s\) by Pythagoras:

\[(\Delta s)^2 = (\Delta x)^2 + (\Delta y)^2 \Rightarrow \Delta s = \sqrt{(\Delta x)^2 + (\Delta y)^2} = \Delta x\,\sqrt{1 + \left(\frac{\Delta y}{\Delta x}\right)^2}\]

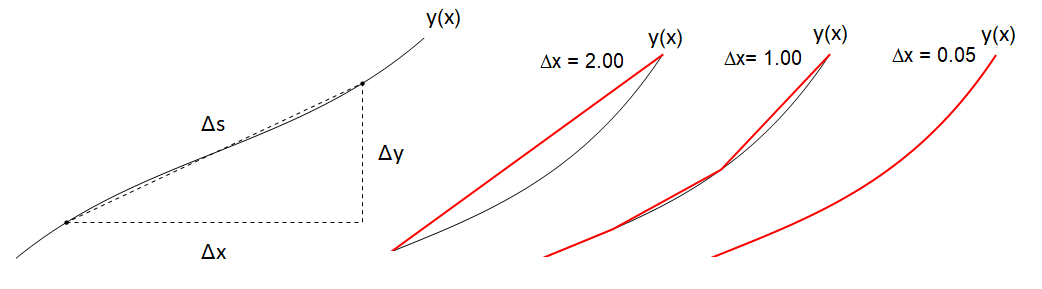
Fig. 2.3 Left Pane: Breaking down path legnth segment \(\Delta s\) into \(x,\, y\) comoonents \(\Delta x,\, \Delta y\), Right Pane: Effect of taking the limit of smaller \(\Delta x\) in finding the path length.

Taking the limit of \(\Delta x\rightarrow 0\) we find:

\[\mathrm{d}s = \mathrm{d}x\, \sqrt{1 + \left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)^2}\]

and therefore to find the path length:

\[L = \int_{x=a}^{x=b} \mathrm{d}s = \int_a^b \sqrt{1 + \left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)^2}\,\mathrm{d}x\]

Taking an example here, lets look at \(y = \cosh(x)\) over the range \(x \in [0,\,1]\), so we find \(\mathrm{d}y/\mathrm{d}x = \sinh(x)\), and therefore:

\[L = \int_0^1 \sqrt{1 + \sinh^2(x)}\,\mathrm{d}x = \int_0^1 \cosh(x)\,\mathrm{d}x = \Big[ \sinh(x) \Big]_0^1 = \sinh(1) \simeq 1.175\dots\]

We might also have a function which is parameterised \(y = y(t),\, x=x(t)\), it is also possible to find an expression for the path length, taking the limit of \(\Delta t \rightarrow 0\):

\[\begin{split}\Delta s &= \Delta t\,\sqrt{\left(\frac{\Delta x}{\Delta t}\right)^2 + \left(\frac{\Delta y}{\Delta t}\right)^2} \\ \Rightarrow \mathrm{d}s &= \mathrm{d}t\, \sqrt{\left(\frac{\mathrm{d}x}{\mathrm{d}t}\right)^2 + \left(\frac{\mathrm{d}y}{\mathrm{d}t}\right)^2}\end{split}\]

An example here would be a circle, parameterised by \(x = R\cos(t),\, y = R\sin(t)\), over the range \(t \in [0,\, 2\pi)\), giving \(\mathrm{d}x/\mathrm{d}t = -R\sin(t),\, \mathrm{d}y/\mathrm{d}t = R\cos(t)\) and therefore:

\[L = \int_0^{2\pi} \sqrt{R^2\sin^2(t) + R^2\cos^2(t)}\,\mathrm{d}t = \int_0^{2\pi} R\,\mathrm{d}x = \Big[ Rt \Big]_0^{2\pi} = 2\pi\,R\]

which gives the result for the circumference of a circle!

2.2. Surfaces of Revolution

Lets now go further, what happens if we take a function and rotate it around an axis, as shown in Fig. 2.4.

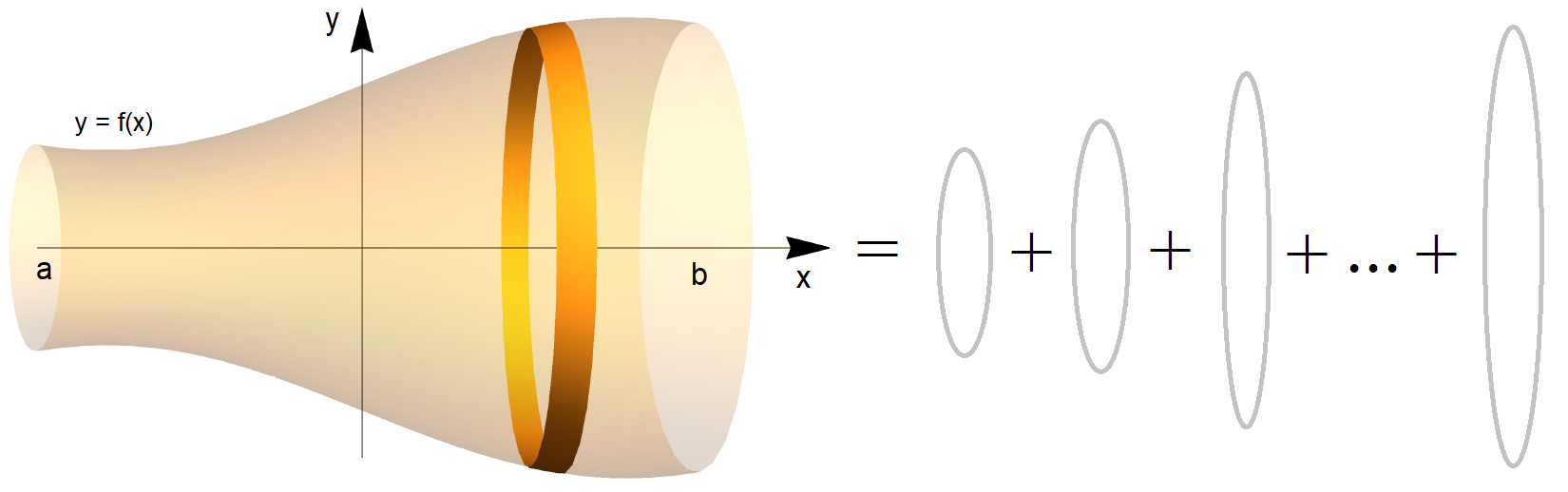
Fig. 2.4 Left Pane: Rotating a function \(y = f(x)\) around the \(x\) axis, over \(x \in [a,\, b]\) producing a solid of revolution, Right Pane: Breaking down the volume into discrete slices, each of width \(\mathrm{d} x\).

To find the volume of such a rotated solid, we need to think about the cross sectional area along the range, which will be \(\pi \,y^2\) since the radius of each slice at \(x\) is \(y(x)\). Then we just need to integrate up these slices \(\pi\,y^2\,\mathrm{d}x\) over the range:

\[V_x = \int_a^b \pi\,y^2\,\mathrm{d}x\]

and we can swap round the axis we rotate over to the \(y\) axis and therefore the radius of each slice would be \(\pi\,x^2\) and therefore:

\[V_y = \int_{y(a)}^{y(b)} \pi\,x^2\,\mathrm{d}y\]

We can also find the surface area of this solid of revolution, if we rotate over the \(x\) acis then this surface area is the circumference of each slice \(2\pi\,y\) multiplied by the path length \(\mathrm{d} s\) along the surface, so we find:

\[A_x = \int_{x=a}^{x=b} 2\pi\,y\,\mathrm{d}s = \int_a^b 2\pi\,y\,\sqrt{1 + \left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)^2}\,\mathrm{d}x\]

We could rotate over the \(y\) axis instead, in which case we just switch the circumference we are interested in to be \(2\pi\,x\) and integrate the path length over the \(y\) axis:

\[A_y = \int_{y(a)}^{y(b)} 2\pi\,x\,\mathrm{d}s = \int_{y(a)}^{y(b)} 2\pi\,x\,\sqrt{1 + \left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)^2}\,\mathrm{d}y\]

As an example, lets find the volume of a cone depicted in Fig. 2.5, with height \(h\) and circular radius \(R\), so \(y = R x / h\) over the range \(x \in [0,\, h]\):

\[\begin{split}V_x = \int_0^h \pi\,\left(\frac{R x}{h}\right)^2\,\mathrm{d}x = \frac{R^2 \,\pi}{h^2}\Big[ \frac{1}{3}x^3\Big]_0^h = \frac{1}{3}\pi \,R^2\,h\\\end{split}\]

which matches the expression we expect and explains where this factor of \(1/3\) comes from!

Likewise we can look at the surface area of this cone, \(y = R x / h \rightarrow \mathrm{d}y/\mathrm{d}x = R / h\) over the range \(x \in [0,\, h]\):

\[\begin{split}A_x &= \int_0^h 2\pi\,\frac{R x}{h}\,\sqrt{1 + \left(\frac{R}{h}\right)^2}\,\mathrm{d}x \\ &= 2\pi \frac{R}{h}\sqrt{1 + \left(\frac{R}{h}\right)^2}\Bigg[ \frac{1}{2}x^2\Bigg]_0^h \\ &= \pi R h\sqrt{1 + \left(\frac{R}{h}\right)^2} = \pi R\sqrt{h^2 + R^2}\end{split}\]

where \(\sqrt{h^2 + R^2}\) is the slant length.

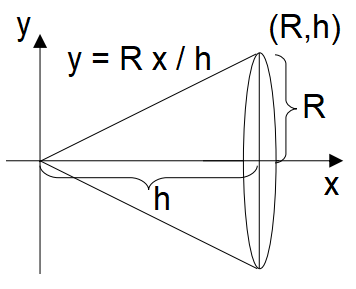
Fig. 2.5 Depiction of a function \(y = R x / h\) and the solid of revolution around the \(x\) axis - a cone.

Likewise if we have parametrised expressions \(x = x(t),\, y = y(t)\), over the range \(t \in [t_1,\, t_2]\) then these expressions become:

\[\begin{split}V_x &= \int_{t_1}^{t_2} \pi\,y^2\,\frac{\mathrm{d}x}{\mathrm{d}t}\,\mathrm{d}t \\ V_y &= \int_{t_1}^{t_2} \pi\,x^2\,\frac{\mathrm{d}y}{\mathrm{d}t}\,\mathrm{d}t \\ A_x &= \int_{t_1}^{t_2} 2\pi\,y\,\sqrt{\left(\frac{\mathrm{d}x}{\mathrm{d}t}\right)^2 + \left(\frac{\mathrm{d}y}{\mathrm{d}t}\right)^2}\,\mathrm{d}t \\ A_y &= \int_{t_1}^{t_2} 2\pi\,x\,\sqrt{\left(\frac{\mathrm{d}x}{\mathrm{d}t}\right)^2 + \left(\frac{\mathrm{d}y}{\mathrm{d}t}\right)^2}\,\mathrm{d}t\end{split}\]

previous

1. Multivariable Calculus

next

3. Vectors and Vector Algebra