.md .pdf

Contents

7. Line Integrals

Following on from the idea of breaking up a function into infintesimal sections \(\mathrm{d} s\), we can think about a path through a vector field \(\bf A(r)\), as depicted in Fig. 7.1. Starting from some vector \(\bf r_A\) we can follow some path through the vector field (which we denote \(C\)), with the path following the field’s direction at each point before finishing at point \(\bf r_B\):

\[I = \int_C {\bf G(r)} \cdot \mathrm{d}{\bf r}\]

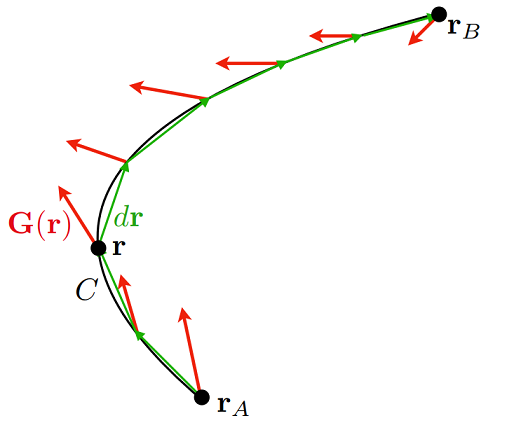
Fig. 7.1 Ilustration of a line integral, with \(I = \int_C {\bf G(r)}\cdot \mathrm{d}{\bf r}\)

We see that that this is a scalar, found from the scalar product of \(\bf G\) with the differential line element \(\mathrm{d}{\bf r}\).

IF we pick a closed path, we call this a Loop Integral:

\[I = \oint_C {\bf G(r)} \cdot \mathrm{d}{\bf r}\]

7.1. Calculating Line Integrals

Whilst the notation for a line integral looks compact, it does not really make it clear how we can evaluate over a path \(C\). In order to make progress, we need to parametrise the path, lets say with some variable \(t\):

\[\begin{split}t &\rightarrow&\, {\bf r}(t) \\ [a,\, b] &\rightarrow&\, \mathbb{R}^3\end{split}\]

which means the path runs \({\bf r_A} = {\bf r}(a) \rightarrow {\bf r_B} = {\bf r}(b)\). Looking at the line element:

\[\begin{split}\mathrm{d}{\bf r}(t) = \begin{pmatrix} \mathrm{d}x (t) \\ \mathrm{d}y (t) \\\mathrm{d}z (t)\end{pmatrix} = \begin{pmatrix} x'\mathrm{d}t \\ y'\mathrm{d}t \\ z'\mathrm{d}t\end{pmatrix} = {\bf r}'(t)\,\mathrm{d} t\end{split}\]

and thus to express this as an integral in a way we can calculate it, with some parameter \(t\):

\[I = \int_C {\bf G}(r) \cdot \mathrm{d}{\bf r} = \int_a^b {\bf G}({\bf r}(t)) \cdot {\bf r}'(t)\,\mathrm{d}t \]

7.1.1. Examples of Line Integrals

As an example lets consider the vector field:

\[\begin{split}{\bf G(r)} = \begin{pmatrix} xy\\ -y^2 \end{pmatrix}\end{split}\]

and look at the line integral over the points \((0,\, 0) \rightarrow (1,2)\) across different paths. Lets pick the parameter \(t\) to be the \(x\) coordinate, so that the path if determined by \(y = f(x), \, x \in [a,\, b]\) such that:

\[\begin{split}{\bf r}(x) = \begin{pmatrix} x \\ f(x) \end{pmatrix}\end{split}\]

Lets consider different paths:

• Straight line path

The function following by this path will be \(y = 2x,\, x \in [0, 1]\), so:

\[\begin{split}{\bf r}(x) = \begin{pmatrix} x \\ 2x \end{pmatrix}\end{split}\]

Thus \({\bf G}({\bf r}(x))\) will be:

\[\begin{split}{\bf G}({\bf r}(x)) = \begin{pmatrix} 2x^2 \\ -4x^2 \end{pmatrix}\end{split}\]

and \({\bf r'}(x)\) is given by:

\[\begin{split}{\bf r}'(x) = \begin{pmatrix} 1 \\ 2 \end{pmatrix}\end{split}\]

so the line integral is found by:

\[\begin{split}I &= \int_C {\bf G}(r) \cdot \mathrm{d}{\bf r} = \int_0^1 {\bf G}({\bf r}(t)) \cdot {\bf r}'(t)\,\mathrm{d}t = \int_0^1 \begin{pmatrix} 2x^2 \\ -4x^2 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} \mathrm{d}x \\ &= \int_0^1 \left( 2x^2 - 8x^2 \right)\,\textrm{d}x = -\int_0^1 6x^2 \,\textrm{d}x = \Big[ -\frac{6}{3}x^3\Big ]_0^1 = -2\end{split}\]

• Curved path following \(y = x^2\)

\[\begin{split}{\bf r}(x) = \begin{pmatrix} x \\ x^2 \end{pmatrix}\end{split}\]

Thus \({\bf G}({\bf r}(x))\) will be:

\[\begin{split}{\bf G}({\bf r}(x)) = \begin{pmatrix} x^3 \\ -x^4 \end{pmatrix}\end{split}\]

and \({\bf r'}(x)\) is given by:

\[\begin{split}{\bf r}'(x) = \begin{pmatrix} 1 \\ 2x \end{pmatrix}\end{split}\]

so the line integral is found by:

\[\begin{split}I &= \int_C {\bf G}(r) \cdot \mathrm{d}{\bf r} = \int_0^1 {\bf G}({\bf r}(t)) \cdot {\bf r}'(t)\,\mathrm{d}t = \int_0^1 \begin{pmatrix} x^3 \\ -x^4 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 2x \end{pmatrix} \mathrm{d}x \\ &= \int_0^1 \left( x^3 - 2x^5 \right)\,\textrm{d}x = \Big[\frac{1}{4}x^4 - \frac{1}{3}x^6 \Big ]_0^1 = -\frac{1}{12}\end{split}\]

• Curved path following \(y = x^{1/2}\)

\[\begin{split}{\bf r}(x) = \begin{pmatrix} x \\ x^{1/2} \end{pmatrix}\end{split}\]

Thus \({\bf G}({\bf r}(x))\) will be:

\[\begin{split}{\bf G}({\bf r}(x)) = \begin{pmatrix} x^{3/2} \\ -x \end{pmatrix}\end{split}\]

and \({\bf r'}(x)\) is given by:

\[\begin{split}{\bf r}'(x) = \begin{pmatrix} 1 \\ \frac{1}{2} x^{-1/2} \end{pmatrix}\end{split}\]

so the line integral is found by:

\[\begin{split}I &= \int_C {\bf G}(r) \cdot \mathrm{d}{\bf r} = \int_0^1 {\bf G}({\bf r}(t)) \cdot {\bf r}'(t)\,\mathrm{d}t = \int_0^1 \begin{pmatrix} x^{3/2} \\ -x \end{pmatrix} \cdot \begin{pmatrix} 1 \\ \frac{1}{2} x^{-1/2} \end{pmatrix} \mathrm{d}x \\ &= \int_0^1 \left( x^{3/2} - \frac{1}{2}x^{1/2} \right)\,\textrm{d}x = \Big[\frac{2}{5}x^{5/2} - \frac{1}{3}x^{3/2} \Big ]_0^1 = \frac{1}{15}\end{split}\]

7.2. Conservative Vector Fields

There is an important class of vector fields, known as conservative vector fields, for which line integrals do not depend on which path is taken from rA to rB, and for which all loop integrals are zero. We see that our example

\[{\bf G(r)} = xy\hat{\bf x} - y^2 \hat{\bf y}\]

is not conservative since the line integrals along different paths from \((0,\, 0)\) to \((1,\,2)\) gave different values.

Whist it is not possible show that for all paths \({\bf r}_A \rightarrow {\bf r}_B\). the line integral gives the same value, simply because there exist infinitely many possible paths. Instead we can use an equivalent definition of conservative fields:

\[\text{Vector Field}\,{\bf G(r)}\,\text{is conservative} \Longleftrightarrow \exists\, \text{Scalar Field}\,\phi({\bf r}),\, \text{s.t.}\,{\bf G} = \nabla \phi\]

To show that a vector field which satisfies this condition is conservative, lets think about a line integral taken along a path \({\bf r}_A \rightarrow {\bf r}_B\), which we have parameterised by the \(t \in [a,\, b]\), where \({\bf}(t=a) = {\bf r}_A\) and \({\bf}(t=b) = {\bf r}_B\)

\[\begin{split}I &= \int_C {\bf G(r)}\cdot \mathrm{d}{\bf r} = \int_{t=a}^{t=b} {\bf G(r)}\cdot {\bf r}'(t) \mathrm{d}t\\ &= \int_{t=a}^{t=b} (\nabla \phi({\bf r}(t)))\cdot {\bf r}'(t) \mathrm{d}t\end{split}\]

However using the fact that the total differential \(\mathrm{d}\phi = \nabla \phi \cdot \mathrm{d}{\bf r}\), then \(\mathrm{d}\phi/\mathrm{d}t = \nabla \phi \cdot \mathrm{d}{\bf r}'\) and thus:

\[\begin{split}I &= \int_{t=a}^{t=b} \frac{\mathrm{d}}{\mathrm{d}t}\phi({\bf r}(t)) \mathrm{d}t \\ &= \Bigg[ \phi({\bf r}(t)) \Bigg]_{t=a}^{t=b} = \phi({\bf r_B}) - \phi({\bf r_A})\end{split}\]

which means that the details of the line integral only depend on the start and finish of the contour, not the path taken. Likewise if we have a conservative vector field and a closed loop integral, then \({\bf r_A} = \bf{r_B}\) and so the integral becomes zero.

For a three dimensional vector field defined on a domain that is simply connected (that is contains no holes) there exists another equivalent definition of conservativeness:

\[\text{Vector Field}\,{\bf G(r)}\,\text{is conservative} \Longleftrightarrow \nabla \times {\bf G} = 0\]

An example, is the vector \({\bf G(r)} = 2xy \hat{\bf x} + (x^2 - 2y)\hat{\bf y} + \hat{\bf z}\) is conservative?

Since G is defined on the entire three-dimensional space \(\mathbb{R}^3\), we can make use the curl criterion, hence

\[\begin{split}\nabla \times {\bf G} &= \begin{pmatrix} \partial_y G_z - \partial_z G_y \\ \partial_z G_x - \partial_x G_y \\ \partial_y G_x - \partial_x G_y\end{pmatrix}\\ &= \begin{pmatrix} 0 - 0 \\ 0 - 0 \\ 2x - 2x\end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}\end{split}\]

Hence since the curl of \(\bf G\) is zero, \(\bf G\) is a conservative vector field, so it must be possible to find a potential \(\phi({\bf r})\) such that \({\bf G} = \nabla \phi\). This means that:

• \(\partial_x \phi = 2xy\)

• \(\partial_x \phi = x^2-2y\)

• \(\partial_x \phi = 1\)

Integrating each of these in turn we find that:

• \(\phi = x^2y + f(y,\,z)\)

• \(\phi = x^2y - y^2 + g(x,\,z)\)

• \(\phi = z + h(z,\,y)\)

Since these all need to be consistent, we find that

\[\phi(x,\,y,\,z) = x^2y - y^2 + z + C\]

up to an additive constant \(C \in \mathbb{C}\). We notice that for the line integral this constant drops out of the calculation anyway.

previous

6. Coordinate Systems

next

8. Multidimensional Integrals