4. Vector Fields¶

A field in a mathematical sense is some function which can be defined within some domain $D$, we will examine fields in two and three spatial dimensions, (but this can be extended to more later as required), therefore $D \subset \mathbb{R}^2$ or $D \subset \mathbb{R}^3$ respectively. If $D$ is not specified, then we assume the whole of the space is being used as the domain.

In a physical sense, a field is some physical quantity which has a value at every point within a space, examples of which include temperature, distances, velocities, acceleations, forces, electric and magnetic fields.

One impoirtant distinction to make between fields is whether they are Scalar, Vector or some other (e.g. Tensor although this is beyond the scope of this course).

4.1. Scalar Fields¶

A scalar field is a physical quantity which has some value (or magnitude) but contains no information about direction, at every point ${\bf r} = (x, \,y, \,z)$ within a domain. Physical examples include pressure and temperature. Mathematically we can write this as a function $\phi$ such that:

\[\begin{split}\phi \,:\, D \,\subset\, \mathbb{R}^3 \,&\longrightarrow&\, \mathbb{R} \\ {\bf r} &\longrightarrow&\, \phi({\bf r})\end{split}\]

4.2. Vector Fields¶

A vector field A scalar field is a physical quantity which has both magnitude and direction, at every point ${\bf r} = (x, \,y, \,z)$ within a domain. Physical examples include velocity, force, and electric and magnetic fields. Mathematically we can write this as a function $\bf A(r)$ such that:

\[\begin{split}\phi \,:\, D \,\subset\, \mathbb{R}^3 \,&\longrightarrow&\, \mathbb{R}^3 \\ {\bf r} &\longrightarrow&\, {\bf A(r)} = \begin{pmatrix} A_x ({\bf r})\\ A_y ({\bf r})\\ A_z ({\bf r}) \end{pmatrix}\end{split}\]

We can picture these fields in Fig. 4.1, outlining the difference between scalar and vecor fields.

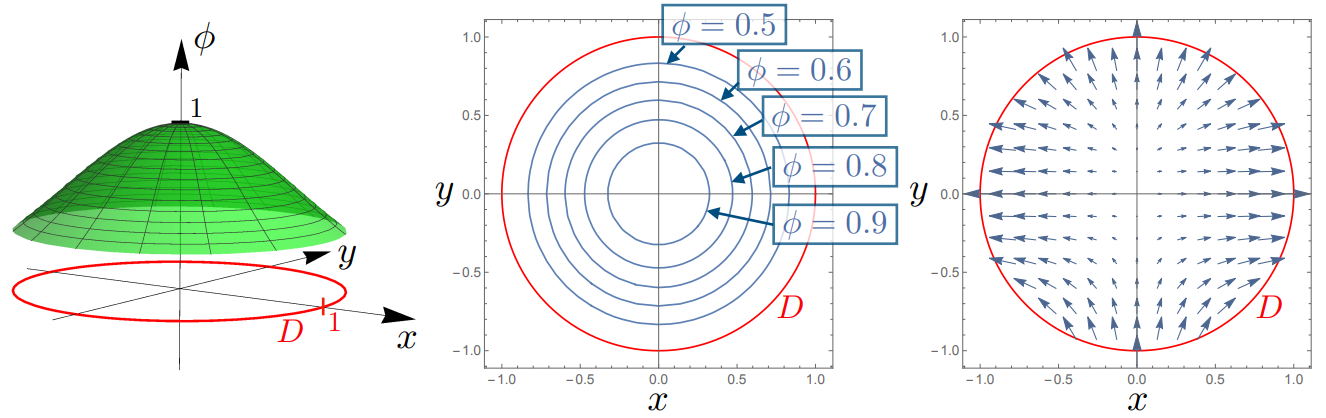
Fig. 4.1 Left Pane: An example of a two-dimensional scalar field, $\phi(x,\, y) = \exp(-(x^2+y^2))$ (plotted in green on the $z$ axis) defined over the domain $D\,:\,x^2 + y^2 \leq 1$ (shown in red on the $(x,\,y)$ plane), Center Pane: Contour lines of the scalar field, showing lines of constant $\phi$ in blue, within the domain $D$, Right Pane: The vector field ${\bf A(r)} = \frac{1}{10}\begin{pmatrix} x\\ y^2 \end{pmatrix}$ over the same domain $D$.¶

4.3. Calculus on Fields¶

4.3.1. Gradient Operator¶

Now that we have defined fields, which can vary according to different parameters at every point within a domain, we can begin to apply our toolkit of mathematical tools, here calculus.

We can find the partial derivatives of fields in a similar way to functions, for example for $\phi = \exp(-(x^2+y^2)$, ${\bf A(r)} = \frac{1}{10}\begin{pmatrix} x\\ y^2 \end{pmatrix}$:

\[\begin{split}\partial_x \phi &= -2x\,\exp(-(x^2+y^2) \\ \partial_y \phi &= -2y\,\exp(-(x^2+y^2) \\ \partial_x {\bf A(r)} &= \frac{1}{10}\begin{pmatrix} 1\\ 0 \end{pmatrix} \\ \partial_y {\bf A(r)} &= \frac{1}{10}\begin{pmatrix} 0\\ 2y \end{pmatrix} \end{split}\]

These partial derivatives measure the change of $\phi$ along the directions of $x$ or $y$, but can we calculate the derivative of $\phi$ along some general direction, characterised by a unit vector $\hat{\bf u}$:

\[\begin{split}\hat{\bf u} = \begin{pmatrix} u_x\\ u_y\\ u_z \end{pmatrix} \end{split}\]

We need a directional derivative, which can tell us about the changes in $\phi$ along each component of $\hat{\bf u}. This leads us to the gradient operator:

\[\begin{split}\nabla = \begin{pmatrix} \partial/\partial x \\ \partial/\partial y \\ \partial/\partial z \end{pmatrix} \end{split}\]

which as an operator needs to act on a scalar field:

\[\begin{split}\nabla \phi = \begin{pmatrix} \partial\phi/\partial x \\ \partial\phi/\partial y \\ \partial\phi/\partial z \end{pmatrix} \end{split}\]

We see that this is now a vector field, which we can resolve in the $\hat{\bf u}$ direction:

\[\hat{\bf u} \cdot \nabla \phi\]

which is our directional derivative of $\phi$ in the $\hat{\bf u}$ direction, which we often write as $\nabla_{\hat{\bf u}} \phi$.

Looking at this expression further:

\[|\nabla_{\hat{\bf u}} \phi| = \hat{\bf u} \cdot \nabla \phi = |\hat{\bf u}||\nabla \phi|\cos (\theta) = |\nabla \phi|\cos (\theta)\]

therefore $|\nabla_{\hat{\bf u}} \phi|$ is maximised when $\theta = 0$ - The gradient $\nabla \phi$ of a scalar field $\phi$ always points toward the direction of maximum increase of $\phi$ (i.e. a maxima).

Likewise the directional derivative is zero when $\theta = \pi/2$, i.e. tangential surfaces, which would be given by $\phi({\bf r}) = C$ which is one dimension lower than the dimension of the problem (therefore in 3D, these would be surface areas, in 2D there would be contour lines).

As example, lets consider $\phi = \exp(-(x^2+y^2)$ defined over the domain $x^2 + y^2 \leq 1$:

\[\begin{split}\nabla \phi = \begin{pmatrix} -2x\,\exp(-(x^2+y^2) \\ -2y\,\exp(-(x^2+y^2) \end{pmatrix} = -2\,\exp(-(x^2+y^2) \begin{pmatrix} x \\ y \end{pmatrix}\end{split}\]

We see that for all $x,\, y$ within the domain, the vector will be directed inwards, as we see in Fig. 4.2.

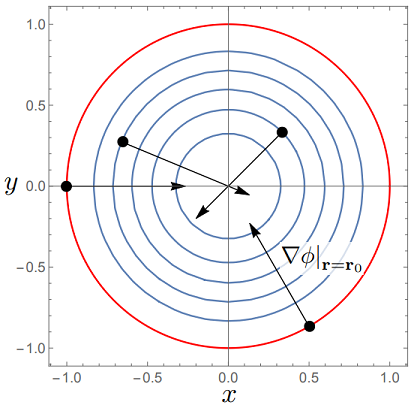
Fig. 4.2 Gradients $\nabla \phi$ for a scalar field $\phi({\bf r}) = \exp(-(x^2+y^2))$ at a few different points along the contour plot (denoted $\bf r=r_0$). The gradients are perpendicular to the contour lines and point toward the direction of the largest increase of $\phi$, which from Fig. 4.1 we know is a maxima.¶

The gradient of $\phi(x,\,y,\,z)$ will therefore be perpendicular to the surface $\phi=c$, and we can use this to find the tangent plane to the surface at a given point. The gradient of $z = z(x,\,y)$ will be perpendicular to the contours of $z$, projected in the $(x,\,y)$ plane, as illustrated in Fig. 4.3.

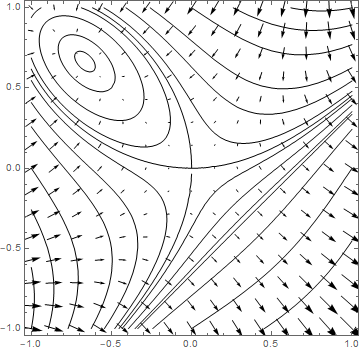
Fig. 4.3 A contour plot of the surface $z = x^3−y^3−2xy+2$, together with the gradient field given by $\nabla z = (3x^2−2y,\,−3y^2−2x,\,0)$.¶

We can always take some surface $z = z(x,\,y)$ and convert it into a scalar field $\phi$ with some surface normal ${\bf n} = \nabla \phi$, for instance $z = x^3−y^3−2xy+2$ means we can write $\phi = x^3−y^3−2xy+2 - z$ and therefore:

\[\begin{split}{\bf n} = \nabla \phi = \begin{pmatrix} 3x^2 - 2y \\ -3y^2 - 2x \\ -1 \end{pmatrix}\end{split}\]

If we want to find the equation of the resulting tangent surface at a given point, say $A:(1,\,1,\,0)$, then we know that the scalar products of all vectors $\begin{pmatrix} x\\y\\z \end{pmatrix}$ on the tangent surface with the surface normal must agree, hence:

\[\begin{split}{\bf n}_A &= \begin{pmatrix} 3-2\\-3-2\\0 \end{pmatrix} = \begin{pmatrix} 1\\-5\\0 \end{pmatrix} \\ {\bf n}_A\cdot \begin{pmatrix} x\\y\\z \end{pmatrix} &= {\bf n}_A\cdot \begin{pmatrix} 1\\1\\0 \end{pmatrix} \Rightarrow x - 5y - z =-4\end{split}\]

Another example would be to find the gradient of the function $f(x,\,y,\,z) = xyz$ at the point $(−2,\,3,\,4)$ and also find the directional derivative of this function in the direction ${\bf v} = (3, \,-4, \,12)$. We can find $\nabla f$:

\[\nabla f = (yz,\,xz,\, xy) \Rightarrow \nabla f\Bigg|_{(−2,\,3,\,4)} = (12,\, -8,\, -6)\]

and therefore the directional derivative is given by:

\[\frac{1}{|{\bf v}|}{\bf v} \cdot \nabla f\Bigg|_{(−2,\,3,\,4)} \Rightarrow \frac{1}{\sqrt{3^2 + 4^2 + 12^2}} (3, \,-4, \,12)\cdot (12,\, -8,\, -6) = -\frac{4}{13}\]

4.4. Total Differential¶

Recall from our discussions about partial derivatives, we can also define a scalar total differential:

\[\mathrm{d}\phi = \frac{\partial \phi}{\partial x} \mathrm{d} x + \frac{\partial \phi}{\partial y} \mathrm{d} y + \frac{\partial \phi}{\partial z} \mathrm{d} z\]

which measures the infinitesimal change of $\phi$ as we change $x, \,y,\,z$ by infinitesimal amounts $\mathrm{d}x, \,\mathrm{d}y,\, \mathrm{d}z$.
Likewise we can define the vectorial line element:

\[\begin{split}\mathrm{d}{\bf r} = \begin{pmatrix} \mathrm{d}x \\\mathrm{d}y\\ \mathrm{d}z\end{pmatrix}\end{split}\]

or to write in a slightly more compact notation:

\[\mathrm{d}\phi = \nabla \phi \cdot \mathrm{d}{\bf r}\]

To find the vector total differential:

\[\mathrm{d}{\bf A} = \frac{\partial {\bf A} }{\partial x} \mathrm{d} x + \frac{\partial {\bf A} }{\partial y} \mathrm{d} y + \frac{\partial {\bf A} }{\partial z} \mathrm{d} z \]

Mathematics for Natural Sciences 2

Vector Fields

Contents